NormaleDefinition Normale
Eine Gerade, die orthogonal zu einem anderen mathematischen Objekt verläuft, z.B. zu einer anderen Gerade, einer Strecke, einer Ebene, einem Kreis oder einer Kurve heißt Normale.
Eine Normale steht senkrecht auf einer Tangente und verläuft durch deren Berührpunkt.
Normale einer Gerade (Funktionsschreibweise)
Gerade 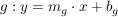 und Normale und Normale 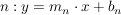
Falls weder 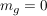 , noch , noch 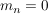 (s.u.), so gilt für die Steigungen (s.u.), so gilt für die Steigungen 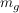 und und 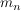 : :
(Diese Formel folgt mit einfachen Überlegungen am Steigungsdreieck.)
Mit dieser Formel läßt sich bequem die Steigung einer Normalen berechnen,
falls die Steigung der Geraden bekannt ist: 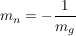 ; ;
die Steigung der Normalen ist daher der negative Kehrbruch der Steigung der Geraden.
Die Fälle 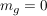 oder oder 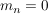 müssen separat betrachtet werden, müssen separat betrachtet werden,
da für einen dieser Fälle entweder die Normale oder die Gerade keine Funktion ist:
Falls 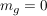 , dann verläuft die Gerade g parallel zur x-Achse, eine Normale dazu ist eine Parallele zur y-Achse und somit keine Funktion. Umgekehrt TODO , dann verläuft die Gerade g parallel zur x-Achse, eine Normale dazu ist eine Parallele zur y-Achse und somit keine Funktion. Umgekehrt TODO
Normale einer Gerade (Vektorschreibweise)
TODO
|