SteigungDer Graph einer linearen Funktion  mit mit
hat die Steigung 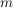 . .
Die Steigung gibt an, ob die Gerade im Koordinatensystem steigt oder fällt.
Will man den Winkel bestimmen, mit dem die Gerade steigt, also ihren Schnittwinkel 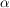 mit der x-Achse, so gilt: mit der x-Achse, so gilt:
Die Steigung 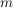 des Graphen stimmt mit der Änderungsrate der Funktionswerte überein: des Graphen stimmt mit der Änderungsrate der Funktionswerte überein:
Beispiel
Der Achsenabschnitt bestimt den Punkt (0|5,5) auf der y-Achse, in dem die Gerade die Achse schneidet.
Der Bruch  ist die Steigung. Die ist so definiert: wenn man von einem bekannten ist die Steigung. Die ist so definiert: wenn man von einem bekannten
Punkt aus (also z.B. dem y-Achsen-Abschnitt) um 1 nach rechts geht, dann muss man um die Steigung hoch
(bei positiver Steigung) oder runter (bei negativer Steigung) gehen, um einen weiteren Punkt zu finden.
Bei Brüchen ist das aber schwer, da 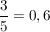 schwer abzulesen ist im Koordinatensystem. schwer abzulesen ist im Koordinatensystem.
Abhilfe: die Steigung ist eine Konstante, d.h. "1 rechts und  nach oben" bedeutet nach oben" bedeutet
dasselbe wie "2 rechts und  nach oben" oder "3 rechts und nach oben" oder "3 rechts und  " u.s.w. " u.s.w.
In Gedanken weitergeführt bis "5 nach rechts und 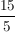 " nach oben - " nach oben - 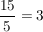 , da kürzt sich die 5 wieder weg. , da kürzt sich die 5 wieder weg.
Was heißt das? Jede Steigung, die als Bruch gegeben ist, kann man also bequem einzeichnen: bei der
Steigung  geht man 5 nach rechts und 3 nach oben, geht man 5 nach rechts und 3 nach oben,
bei der Steigung  würde man 4 nach rechts und 7 nach oben gehen, würde man 4 nach rechts und 7 nach oben gehen,
und bei negativen Steigungen: 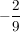 eben 9 nach rechts und 2 nach unten. eben 9 nach rechts und 2 nach unten.
siehe auch: Gerade, Achsenabschnitt
|