Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
| www.matheraum.de
Wahrscheinlichkeitstheorie (Bauer)
Aufgabenblatt 2
Abgabe: Fr 15.06.2007 10:00 | 18.05.2007 | Dieser Übungszettel enthält die Aufgaben aus Kapitel I, § 3. Verteilung, Erwartungswert, Varianz, Jensensche Ungleichung.
Die Aufgaben sind diesmal sehr technisch, der nächste Aufgabenzettel wird wieder interessanter. | | Aufgabe 1 | Eine 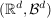 -Zufallsvariable X auf einem W-Raum -Zufallsvariable X auf einem W-Raum 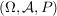 nehme nur abzählbar viele Werte nehme nur abzählbar viele Werte 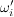 , , 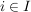 an (I abzählbar). an (I abzählbar).
Man zeige, dass
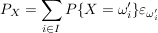
| | Aufgabe 2 | Man betrachte den Laplaceschen W-Raum 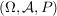 aus § 2, Situation 1 (b); dort ist aus § 2, Situation 1 (b); dort ist 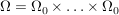 das Produkt von m Kopien einer n-elementigen Menge das Produkt von m Kopien einer n-elementigen Menge 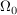 (z.B. von Kugeln). (z.B. von Kugeln).
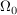 sei die Vereinigung zweier fremder Teilmengen sei die Vereinigung zweier fremder Teilmengen 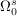 und und  (z.B. der Menge aller schwarzen bzw. weißen Kugeln). (z.B. der Menge aller schwarzen bzw. weißen Kugeln).
Für jedes 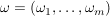 bezeichne bezeichne 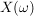 die Anzahl aller Indizes die Anzahl aller Indizes 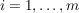 mit mit 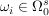 . .
Man bestimme die Verteilung der Zufallsvariablen X.
Situation § 2, 1 (b):
In einer Urne befinden sich gut durchmischt n gleichartige Kugeln in den Farben Schwarz und Weiß, etwa s schwarze und w weiße (s+w=n). Man zieht willkürlich 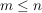 Kugeln und legt jede gezogene Kugel sofort wieder in die Urne zurück. Kugeln und legt jede gezogene Kugel sofort wieder in die Urne zurück.
Gefragt ist die Wahrscheinlichkeit, dass darunter genau  schwarze Kugeln sind. schwarze Kugeln sind.
| | Aufgabe 3 | Sei 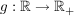 eine symmetrisierte, Borel-meßbare, auf eine symmetrisierte, Borel-meßbare, auf 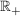 isotone Funktion mit g(x)>0 für alle isotone Funktion mit g(x)>0 für alle  . .
Ferner sei X eine reelle Zufallsvariable.
Man beweise die folgende Verallgemeinerung der  Chebyshev-Markovschen Ungleichung (vgl. MI, (20.1)): Chebyshev-Markovschen Ungleichung (vgl. MI, (20.1)):
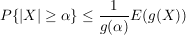
( ) ) | | Aufgabe 4 | Es sei X eine Zufallsvariable auf 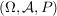 mit Werten in mit Werten in 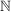 . .
Man beweise die Gleichheit
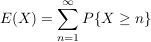
sowohl auf elementarem Weg als auch mit Hilfe von MI (23.10).
MI (23.10): 
| | Aufgabe 5 | In der Situation des Satzes 3.8 (siehe Satz "rechtsseitige Tangenten konvexer Funktionen verlaufen unterhalb des Graphen" im MatheBank-Artikel  konvex) zeige man, dass für beliebige Punkte konvex) zeige man, dass für beliebige Punkte 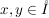 mit x<y die Ungleichungen mit x<y die Ungleichungen
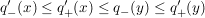
gelten. | | Aufgabe 6 | Aus der  Jensenschen Ungleichung (3.23) folgere man für eine konvexe Funktion q auf einem offenen Interval Jensenschen Ungleichung (3.23) folgere man für eine konvexe Funktion q auf einem offenen Interval  die folgende elementare Form dieser Ungleichung: die folgende elementare Form dieser Ungleichung:
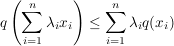
für je endlich viele Punkte 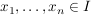 und reelle Zahlen und reelle Zahlen  mit mit 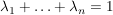 . .
Gilt diese Aussage auch, wenn I ein beliebiges Intervall und q hierauf konvex ist? | | Aufgabe 7 | Man beweise, dass der Satz 3.9 (= Jensensche Ungleichung) auch für ein beliebiges Intervall Jensensche Ungleichung) auch für ein beliebiges Intervall  gültig ist. gültig ist.
Hierzu analysiere man das Verhalten von q in einem Endpunkt von I. Insbesondere zeige man zunächst, dass eine konvexe Funktion q auf I nach unten halbstetig ist, d.h. dass für jedes 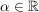 die Menge aller die Menge aller 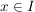 mit mit 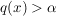 offen in I ist. offen in I ist. |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|