www.vorkurse.de
Ein Projekt von vorhilfe.de
Die Online-Kurse der Vorhilfe

E-Learning leicht gemacht.
Hallo Gast! [ einloggen | registrieren ]
Startseite · Mitglieder · Teams · Forum · Wissen · Kurse · Impressum
Forenbaum
^ Forenbaum
Status Mathe-Vorkurse
  Status Organisatorisches
  Status Schule
    Status Wiederholung Algebra
    Status Einführung Analysis
    Status Einführung Analytisc
    Status VK 21: Mathematik 6.
    Status VK 37: Kurvendiskussionen
    Status VK Abivorbereitungen
  Status Universität
    Status Lerngruppe LinAlg
    Status VK 13 Analysis I FH
    Status Algebra 2006
    Status VK 22: Algebra 2007
    Status GruMiHH 06
    Status VK 58: Algebra 1
    Status VK 59: Lineare Algebra
    Status VK 60: Analysis
    Status Wahrscheinlichkeitst

Gezeigt werden alle Foren bis zur Tiefe 2

Navigation
 Startseite...
 Neuerdings beta neu
 Forum...
 vorwissen
   Einstieg
   
   Index aller Artikel
   
   Hilfe / Dokumentation
   Richtlinien
   Textgestaltung
 vorkurse...
 Werkzeuge...
 Nachhilfevermittlung beta...
 Online-Spiele beta
 Suchen
 Verein...
 Impressum
Das Projekt
Server und Internetanbindung werden durch Spenden finanziert.
Organisiert wird das Projekt von unserem Koordinatorenteam.
Hunderte Mitglieder helfen ehrenamtlich in unseren moderierten Foren.
Anbieter der Seite ist der gemeinnützige Verein "Vorhilfe.de e.V.".
Partnerseiten
Weitere Fächer:

Open Source FunktionenplotterFunkyPlot: Kostenloser und quelloffener Funktionenplotter für Linux und andere Betriebssysteme
Assoziativgesetz
Mach mit! und verbessere/erweitere diesen Artikel!
Artikel • Seite bearbeiten • Versionen/Autoren

Assoziativgesetz

(Weitergeleitet von assoziativ)

Assoziativgesetz:

Bei einer Summe oder einem Produkt von mehreren Zahlen ist es gleichgültig, welche benachbarten Zahlen man zuerst addiert bzw. multipliziert.

$ a+b+c = (a+b)+c=a+(b+c) $

$ a\cdot{}b\cdot{}c=(a\cdot{}b)\cdot{}c=a\cdot{}(b\cdot{}c) $


Assoziativgesetz der Addition:

Bei einer Summe ist es gleichgültig, welche benachbarten Summanden man zuerst addiert.

$ a+b+c = (a+b)+c=a+(b+c) $

Beispiele:

a) 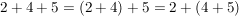$ 2+4+5=(2+4)+5=2+(4+5) $

b) 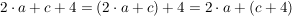$ 2\cdot{}a+c+4=(2\cdot{}a+c)+4=2\cdot{}a+(c+4) $

c) $ \wurzel{3+x} + 5+d=(\wurzel{3+x}+5)+d=\wurzel{3+x}+(5+d) $

d) $ 3-a+a=3+(-a)+a=(3-a)+a=3+(a-a)=3 $

Das Assoziativgesetz erlaubt uns also in einer Summe beliebig Klammern setzen zu dürfen. Besonders praktisch ist das Assoziativgesetz, wenn durch geschicktes Klammern Terme wegfallen, so wie im letzen Beispiel.

Assoziativgesetz der Multiplikation:

Bei einem Produkt ist es gleichgültig, welche benachbarten Faktoren man zuerst multipliziert.

$ a\cdot{}b\cdot{}c=(a\cdot{}b)\cdot{}c=a\cdot{}(b\cdot{}c) $

Beispiele:

a) 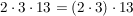$ 2\cdot{}3\cdot{}13=(2\cdot{}3)\cdot{}13 $

b) 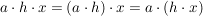$ a\c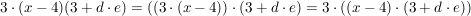d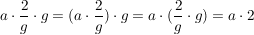ot{}h\cdot{}x=(a\cdot{}h)\cdot{}x=a\cdot{}(h\cdot{}x) $

c) $ 3\cdot{}(x-4)(3+d\cdot{}e)=((3\cdot{}(x-4))\cdot{}(3+d\cdot{}e)=3\cdot{}((x-4)\cdot{}(3+d\cdot{}e)) $

d) $ a\cdot{}\bruch{2}{g}\cdot{}g=(a\cdot{}\bruch{2}{g})\cdot{}g=a\cdot{}(\bruch{2}{g}\cdot{}g)=a\cdot{}2 $

Das Assoziativgesetz erlaubt uns also in einem Produkt beliebig Klammern setzen zu dürfen. Besonders praktisch ist es, wenn durch geschicktes Klammern Terme wegfallen, so im vierten Beispiel.

siehe auch Distributivgesetz, Kommutativgesetz, Rechengesetze

Erstellt: Di 07.09.2004 von Andi
Letzte Änderung: Mo 04.09.2006 um 09:20 von informix
Artikel • Seite bearbeiten • Versionen/Autoren • Titel ändern • Artikel löschen • Quelltext
^ Seitenanfang ^
www.vorkurse.de
[ Startseite | Mitglieder | Teams | Forum | Wissen | Kurse | Impressum ]