RechengesetzDefinition Rechengesetze bei Zahlen
Schule
Zwischen den Zahlen der Zahlenmenge werden die Verknüpfungen "+", die Addition, und "*", die Multiplikation, sowie ihre Umkehrungen "-", die Subtraktion, und "/" oder ":", die Division, definiert.
Addition

a nennt man den 1. Summand und b den 2. Summand.
Die Addition ist in allen Zahlbereichen uneingeschränkt ausführbar.
Rechengesetze
Für beliebige Zahlen a, b, und c gilt:
Kommutativgesetz: a + b = b + a
Assoziativgesetz: (a + b) + c = a + (b + c)
neutrales Element 0: a + 0 = 0 + a = a
Subtraktion

a nennt man den Minuend und b den Subtrahend.
Die Subtraktion ist nicht in allen Zahlenbereichen uneingeschränkt ausführbar.
Falls sie ausführbar ist, ist sie eindeutig:
Für jede Zahl a gilt:
a - a = 0 und a - 0 = a; man nennt (-a) das inverse Element zur Zahl a.
Der Zusammenhang zwischen Addition und Subtraktion ergibt sich aus folgenden Beziehungen:
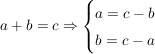
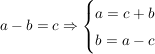
Multiplikation

a nennt man den 1. Faktor und b den 2. Faktor.
Die Multiplikation ist in allen Zahlbereichen uneingeschränkt ausführbar.
Rechengesetze
Für beliebige Zahlen a, b, und c gilt:
Kommutativgesetz: a * b = b * a
Assoziativgesetz: (a * b) * c = a * (b * c)
neutrales Element 1: a * 1 = 1 * a = a
Für jede Zahl a gilt: a * 0 = 0 = * a * 0
Außerdem gilt: Ein Produkt hat genau dann den Wert 0, wenn mindestens einer der Faktoren 0 ist.
Beispiel
(x-2)*(x+3)=0  x-2=0 oder x+3=0 x-2=0 oder x+3=0  x = 2 oder x = -3 x = 2 oder x = -3
Division

a nennt man den Dividend und b den Divisor.
Die Division ist nicht in allen Zahlbereichen uneingeschränkt ausführbar.
Falls sie ausführbar ist, ist sie eindeutig. Die Division durch Null ist in allen Zahlbereichen nicht ausführbar, da in diesen Fällen der Wert des Quotienten nicht existiert oder nicht eindeutig bestimmbar ist.
Für jede Zahl a gilt: a : 1 = a
Für jede Zahl a 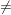 0 gilt: a : a = 1 ; 0 : a = 0; 0 gilt: a : a = 1 ; 0 : a = 0;  ist das inverse Element zu a. ist das inverse Element zu a.
Der Zusammenhang zwischen Multiplikation und Division ergibt sich aus folgenden Beziehungen:


Verbindung der vier Grundrechenarten
Treten in einer Aufgabe Additionen und/oder Subtraktionen (Strichrechnungen) sowie Multiplikationen und/oder Divisionen (Punktrechnungen) gleichzeitig auf, so wird vereinbart, dass Punktrechnungen vor Strichrechnungen ausgeführt werden.
Es gelten im Zusammenhang mit Klammern die Distributivgesetze
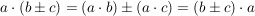
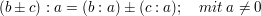
Universität
Division komplexer Zahlen
|