Benutzer:tobit09/Stochastik1Stochastisches Modellieren für Einsteiger
 0. Einleitung 0. Einleitung  Inhaltsverzeichnis Inhaltsverzeichnis  2. Ereignisse E 2. Ereignisse E
1. Ergebnismengen 
a) Ergebnismengen
Am Anfang der Modellierung eines stochastischen Vorganges aus der realen Welt steht die geeignete Wahl einer Ergebnismenge (/Grundmenge/Ergebnisraum/Grundraum)  . Diese enthält als Elemente genau alle möglichen Ausgänge (Ergebnisse) des stochastischen Vorganges. . Diese enthält als Elemente genau alle möglichen Ausgänge (Ergebnisse) des stochastischen Vorganges.
Beispiel: Wurf eines Würfels
Die möglichen Ausgänge sind:
1 gewürfelt, 2 gewürfelt, 3 gewürfelt, 4 gewürfelt, 5 gewürfelt, 6 gewürfelt.
Also könnten wir wählen:
 . .
Da es etwas unhandlich ist, immer dieses "gewürfelt" mitzuschleppen, können wir z.B. den Ausgang "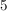 gewürfelt" mit gewürfelt" mit 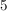 abkürzen. In diesem Sinne lauten die möglichen Ausgänge: abkürzen. In diesem Sinne lauten die möglichen Ausgänge:
1,2,3,4,5,6
Somit erhalten wir als sinnvolle Wahl von  : :
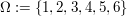 . .
Weiteres Beispiel: Aus einer Urne mit 3 schwarzen und einer weißen Kugel wird eine Kugel gezogen.
Hier könnten wir als mögliche Ausgänge ansehen:
schwarze Kugel gezogen, weiße Kugel gezogen.
Abkürzen könnten wir diese beiden Ausgänge durch s bzw. w. In diesem Sinne könnten wir wählen:
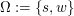 . .
Alternativ könnten wir als Ausgang genau erfassen, welche der vier Kugeln gezogen wird. Dazu könnten wir uns die Kugeln von 1 bis 4 durchnummeriert denken. Z.B. könnten wir die schwarzen Kugeln von 1 bis 3 nummerieren und die weiße Kugel mit der Nummer 4 versehen. Nach dieser Betrachtungsweise wären die möglichen Ausgänge:
1,2,3,4.
Wir würden also
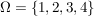
wählen.
Aufgabe 1: Geben Sie geeignete Ergebnismengen für folgende Vorgänge an:
(i) Eine Münze mit einer Zahl auf der einen und einem Bild auf der anderen Seite wird geworfen.
(ii) Ein Skatspiel bestehend aus 32 Karten (7,8,9,10,Bube,Dame,König,As in jeder der Farben Pik,Kreuz,Herz,Karo) wird gemischt und anschließend die oberste Karte gezogen.
(iii) Ein Glücksrad wird gedreht, dessen eine Hälfte ein Nietenfeld ist und dessen andere Hälfte wiederum je zur Hälfte ein Trostpreisfeld und ein Hauptpreisfeld enthält.
Lösungsvorschlag
b) Ergebnismengen aus Tupeln
Zunächst wiederholen wir unabhängig von stochastischen Anwendungen die Mengennotationen im Zusammenhang mit Tupeln:
Beispiel: Was bedeutet das kartesische Produkt 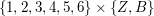 ? ?
Das ist die Menge aller 2-Tupel (Paare) 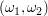 mit mit 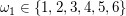 und und 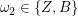 . Also . Also
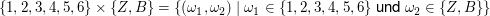 . .
Ein Element dieser Menge wäre z.B. 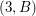 (denn (denn 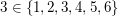 und und 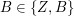 ). Wir können auch alle Elemente explizit aufzählen: ). Wir können auch alle Elemente explizit aufzählen:
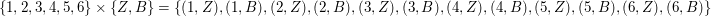 . .
Weiteres Beispiel: Was bedeutet 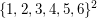 ? ?
Das ist eine Abkürzung für 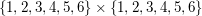 . Also . Also
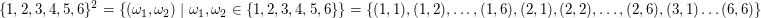 . .
Aufgabe 2: Stellen Sie die Menge aller 3-Tupel (Tripel) von Elementen von 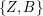 auf mehrere Arten dar. auf mehrere Arten dar.
Lösungsvorschlag
Kommen wir nun zur Bedeutung von Tupeln für die Wahl von Ergebnismengen. Besteht ein stochastischer Gesamtvorgang aus mehreren Einzelvorgängen, so bietet sich die Wahl einer Ergebnismenge aus Tupeln an.
Beispiel: Erst wird ein Würfel, dann eine Münze geworfen.
Als Abkürzungen für mögliche Ausgänge könnten wir 2-Tupel (Paare) wie 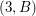 betrachten, die dafür stehen, dass eine 3 gewürfelt und mit der Münze Bild geworfen wurde. Alle möglichen Ausgänge sind dann die Paare betrachten, die dafür stehen, dass eine 3 gewürfelt und mit der Münze Bild geworfen wurde. Alle möglichen Ausgänge sind dann die Paare 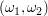 mit mit 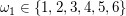 und und 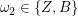 . Wir erhalten so als Ergebnismenge . Wir erhalten so als Ergebnismenge
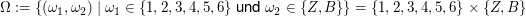 , ,
die wir schon als Beispiel betrachtet haben.
Ähnlich kann man sich überlegen, dass 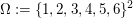 eine geeignete Ergebnismenge für das zweimalige Werfen eines Würfels ist. Genauso lässt sich mit dieser Menge auch das gleichzeitige Werfen mit zwei Würfeln (die man sich gedanklich als mit 1 und 2 durchnummeriert vorstellt) modellieren. eine geeignete Ergebnismenge für das zweimalige Werfen eines Würfels ist. Genauso lässt sich mit dieser Menge auch das gleichzeitige Werfen mit zwei Würfeln (die man sich gedanklich als mit 1 und 2 durchnummeriert vorstellt) modellieren.
Aufgabe 3: Geben sie eine Ergebnismenge für das 10-malige Werfen einer Münze an.
Lösungsvorschlag
Manchmal sind nicht alle Tupel eines kartesischen Produktes mögliche Ausgänge und damit Elemente von  . .
Beispiel: Aus obiger Urne mit 3 schwarzen und einer weißen Kugel werden ohne Zurücklegen zwei Kugeln gezogen.
Wenn wir uns die Kugeln wieder von 1 bis 4 durchnummeriert denken, können wir die möglichen Ausgänge als Paare 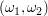 von Zahlen von 1 bis 4 ansehen, deren beiden Einträge von Zahlen von 1 bis 4 ansehen, deren beiden Einträge 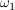 und und 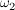 verschieden sind (da nicht zwei mal die gleiche Kugel gezogen werden kann). Als Ergebnismenge erhalten wir so verschieden sind (da nicht zwei mal die gleiche Kugel gezogen werden kann). Als Ergebnismenge erhalten wir so
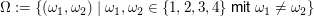 . .
Aufgabe 4: Die Karten eines Skat-Spiels werden gemischt und anschließend vom Stapel die obersten drei Karten gezogen. Geben Sie eine geeignete Grundmenge an. Nehmen sie dazu die Karten als von 1 bis 32 durchnummeriert an.
Lösungsvorschlag
|