Benutzer:tobit09/Stochastik2Stochastisches Modellieren für Einsteiger
 1. Ergebnismengen 1. Ergebnismengen   Inhaltsverzeichnis Inhaltsverzeichnis  3. Zähldichten p und Wahrscheinlichkeits-Verteilungen P 3. Zähldichten p und Wahrscheinlichkeits-Verteilungen P
2. Ereignisse 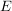
Unter einem Ereignis aus der realen Welt wollen wir etwas verstehen, das bei einem stochastischen Vorganges je nach Ausgang eintritt oder nicht eintritt. Beispiele wären "gerade Zahl gewürfelt" beim Würfelwurf oder "Farbe Pik gezogen" beim Ziehen einer Karte vom Stapel eines Skat-Spiels.
Um vom zugehörigen mathematischen Ereignis 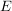 sprechen zu können, muss man sich zunächst auf eine Ergebnismenge sprechen zu können, muss man sich zunächst auf eine Ergebnismenge  für den stochastischen Vorgang festlegen. Dann verstehen wir unter dem mathematischen Ereignis für den stochastischen Vorgang festlegen. Dann verstehen wir unter dem mathematischen Ereignis 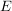 die Menge aller die Menge aller 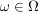 , die für Ausgänge stehen, bei denen das Ereignis aus der realen Welt eintritt. , die für Ausgänge stehen, bei denen das Ereignis aus der realen Welt eintritt.
Beispiel: "gerade Zahl gewürfelt" beim Würfelwurf
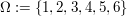
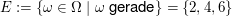
Weiteres Beispiel: "Farbe Pik gezogen" beim Ziehen einer Karte vom Stapel eines Skat-Spiels
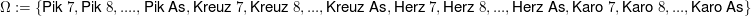
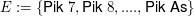
Oder:
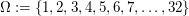
Annahme: Die 7 Pik-Karten haben die Nummern von 1 bis 7 erhalten.
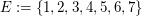
Aufgabe 5: Geben Sie die zugehörigen mathematischen Ereignisse 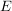 an: an:
(i) "keine Niete erdreht" beim Glücksrad mit den Feldern Niete, Trostpreis und Hauptpreis
(ii) "schwarze Kugel gezogen" beim Ziehen einer Kugel aus einer Urne mit 3 schwarzen und einer weißen Kugel bei Wahl von 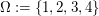 , wobei die schwarzen Kugeln die Nummern 1, 2 und 3 und die weiße Kugel die Nummer 4 erhalte , wobei die schwarzen Kugeln die Nummern 1, 2 und 3 und die weiße Kugel die Nummer 4 erhalte
(iii) "schwarze Kugel gezogen" beim Ziehen einer Kugel aus einer Urne mit 3 schwarzen und einer weißen Kugel bei Wahl von 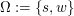
Lösungsvorschlag
Schauen wir uns noch ein paar Ereignisse bei stochastischen Vorgängen an, deren Ausgänge durch Tupel beschrieben werden:
Beispiel: "Augensumme gerade" beim zweifachen Würfelwurf
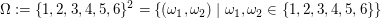
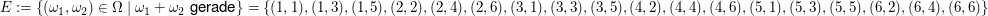
Aufgabe 6: Geben Sie die zugehörigen mathematischen Ereignisse 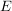 an: an:
(i) "erste Zahl gerade" beim zweifachen Würfelwurf
(ii) "im ersten und letzten Wurf landet die Münze auf der gleichen Seite" beim 10-fachen Münzwurf
(iii) "zwei schwarze Kugeln gezogen" beim zweifachen Ziehen ohne Zurücklegen aus einer Urne mit 3 schwarzen und einer weißen Kugel
(iv) "erst Pik, dann zweimal Herz gezogen" beim Ziehen von 3 verschiedenen Karten eines Skat-Spiels
Lösungsvorschlag
|