trigonometrische FunktionEigenschaften der trigonometrischen Funktionen
Sinusfunktion:
Kosinusfunktion:
Schule
Aus der Definition der beiden Funktionen am Einheitskreis liest man ab, dass
- der Wertebereich beider Funktionen
![$ \IW = [-1;+1] $ $ \IW = [-1;+1] $](/teximg/8/5/00388158.png) ist; ist;
- die Sinusfunktion punktsymmetrisch zum Ursprung ist:
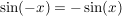 ; ;
- die Kosinusfunktion achsensymmetrisch zur y-Achse ist:
 ; ;
- beide Funktionen periodisch sind mit einer Periodenlänge von
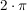 : :
- sich folgende spezielle Funktionswerte als sehr nützlich erweisen:
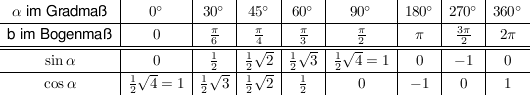
Dabei gilt für die Umrechnung von Gradmaß ins Bogenmaß: 
Ableitung der Sinus- und Kosinusfunktion
Vergleicht man die beiden Graphen, so erkennt man, dass die Kosinusfunktion
exakt den Steigungsverlauf der Sinusfunktion widerspiegelt:
An den Extremstellen von 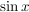 hat hat 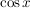 die Nullstellen, die Nullstellen,
die Nullstellen von 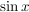 sind zugleich auch ihre Wendepunkte, dort erreicht sind zugleich auch ihre Wendepunkte, dort erreicht 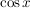 seine Extremwerte. seine Extremwerte.
Analog:
An den Extremstellen von 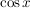 hat hat 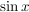 die Nullstellen, die Nullstellen,
die Nullstellen von 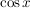 sind zugleich auch ihre Wendepunkte, dort erreicht sind zugleich auch ihre Wendepunkte, dort erreicht 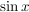 seine Extremwerte. seine Extremwerte.
Es gilt offenbar:
(Beweis mit Hilfe der Additionstheoreme und dem Grenzwert der Sekantensteigungen)
Die Ableitung der allgemeinen Sinus- und Kosinusfunktion erhält man mit der Kettenregel:
Stammfunktion der Sinus- und Kosinusfunktion
Bemerkungen.
siehe auch: Additionstheorem
Beispiele.
Beweis.
Universität
Bemerkungen.
Beispiele.
Beweis.
siehe auch: ![Link auf "http://de.wikipedia.org/wiki/Formelsammlung_Trigonometrie" [link]](/images/popup.gif) Formelsammlung Formelsammlung
siehe auch: Tangensfunktion
|