dynamischDas Wort Dynamik (altgr. dýnamis - Kraft) beschreibt das zeitbezogen geänderte Verhalten eines Objektes im offenen Zustandsraum.
 mit der Lösung mit der Lösung 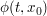 für alle für alle 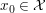 insofern insofern 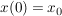 und und 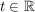 hier definiert sind. hier definiert sind.
Bei diesem Objekt ist es gleichgültig, ob es sich um ein natürliches (z.B. Lebewesen) oder künstliches System handelt. Auch kann die Kraft zu einem Zeitpunkt, die diese Verhaltensänderung hervorruft, vom Inneren des Systems selbst ausgesandt werden (dynamisches Eigenverhalten) oder von außen einwirken.
Die Beschreibung erfolgt zumeist modellhaft mit mathematischen Mitteln in der Form einer Differenzialgleichung oder Differenzengleichung. Es finden natürlich auch andere Beschreibungsformen An- und Verwendung.
Beispiele für die mathematische Beschreibung von Systemen aus der Aerodynamik, Elektrodynamik, Thermodynamik ebenso wie in der Zahlentheorie und Stochastik sind in einschlägiger Fachliteratur zu finden.
Weiterer Hinweis: Wikipedia: Dynamik
zur Übersicht Regelungstechnik
|