VietaSatz von Vieta
Voraussetzungen und Behauptung:
Gegeben sei eine quadratische Funktion 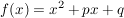
Gesucht seien die Nullstellen 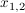
Dann gilt:
mit  und und 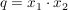
Bemerkungen
Damit erhält man eine sehr schnelle Methode, Nullstellen "durch Hingucken" zu bestimmen.
Leider funktioniert dies Verfahren nur bei ganzen Zahlen p und q, die nicht zu groß sind.
Da aber in der Schule die Nullstellen häufig im Bereich [[-20|20] liegen, kann man mit ein wenig Training die p/q-Formel umgehen und damit die Rechnung beschleunigen.
Beispiele
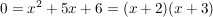 weil 2+3=5 und 2*3=6 weil 2+3=5 und 2*3=6 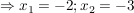
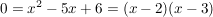 weil -2-3=-5 und -2*(-3)=6 weil -2-3=-5 und -2*(-3)=6 
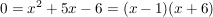 weil -1+6=5 und -1*6=-6 weil -1+6=5 und -1*6=-6 
 weil 1-6=5 und 1*(-6)=6 weil 1-6=5 und 1*(-6)=6 
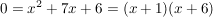 weil 1+6=7 und 1*6=6 weil 1+6=7 und 1*6=6 
Beweis
ergibt sich durch Ausrechnen:

|