PyramidenaufgabeDie folgende Aufgabe könnte in dieser Form als Abituraufgabe gestellt werden;
hier geben wir eine Musterlösung mit Erläuterungen an.
Die Quelle dieser Aufgabe ist dem Verfasser nicht bekannt.
In einem kartesischen Koordinatensystem sind die Punkte A(6;0;0), B(0;6;0),  und D(3;-3;8) gegeben. und D(3;-3;8) gegeben.
1. a) Bestimmen Sie 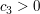 so, dass der Punkt C vom Punkt A die Entfernung 10 LE besitzt! so, dass der Punkt C vom Punkt A die Entfernung 10 LE besitzt!
1. b) Zeichnen Sie die Punkte A, B, C in ein Koordinatensystem und zeichnen Sie ihre Verbindungsstrecken als Spuren einer Ebene E! Bestimmen Sie eine Gleichung von E in Normalenform!
1. c) Bestimmen Sie rechnerisch eine Gleichung der Innenwinkelhalbierenden w des Winkels BCA, den Schnittpunkt S von w mit der Geraden AB sowie den Winkel  von w mit AB! von w mit AB!
Zeichnen Sie w und S in das Koordinatensystem von Teilaufgabe 1b und deuten Sie das Ergebnis geometrisch!
2. a) Die Punkte A, B, C und der Ursprung 0 bilden eine Pyramide. Berechen Sie das Volumen dieser Pyramide!
2. b) Zeichnen Sie das Viereck ABCD in das Koordinatensystem von 1b und zeigen Sie, dass das Viereck ABCD ein Trapez ist! Berechen Sie den Flächeninhalt dieses Trapezes!
3. Die Ebene E': x+y-z-6=0 schneidet die Ebene E (siehe Aufgabe 1b) in einer Geraden s. Zeigen Sie, dass s=AB gilt, und zeichnen Sie E' mit Hilfe ihrer Spuren in das Koordinatensystem von Aufgabe 1b.
Lösung:
1. a) Punkt C
mit 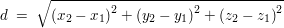 als Abstandformel ergibt sich: als Abstandformel ergibt sich:
1. b) Ebenengleichung
erster Lösungsweg:
Da die drei Ecken des Dreiecks auf den Koordinatenebenen liegen, kann man die Achsenabschnittsform der Geradengleichung in Betracht ziehen:
mit 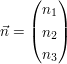 dem Normalenvektor der Ebene. dem Normalenvektor der Ebene.
Die Kehrwerte der oben gegebenen Koeffizienten ergeben die Koordinaten der Spurpunkte nach folgendem Schema:
Man kann dann ein unterbestimmtes Gleichungssystem aufstellen:
Man berechnet die 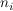 in Abhängigkeit von in Abhängigkeit von 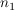 und wählt und wählt 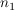 so, dass sich kleine ganze Zahlen ergeben: so, dass sich kleine ganze Zahlen ergeben:
Mit  ist diese Bedingung erfüllt und es folgt: ist diese Bedingung erfüllt und es folgt:
Alternativ kann man auch die 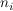 in Abhängigkeit von in Abhängigkeit von  berechnen und das kleinste gemeinsame Vielfache berechnen und das kleinste gemeinsame Vielfache 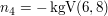 wählen. wählen.
Mit 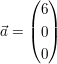 kann man nun die Normalenform der Ebenengleichung aufstellen: kann man nun die Normalenform der Ebenengleichung aufstellen:
zweiter Lösungsweg:
Man benutzt die Normalenform der Ebene E: 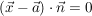
Aufhängepunkt sei A mit dem Ortsvektor 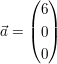
Die Richtungsvektoren 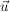 und und 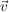 ergeben sich aus den Verbindugnsvektoren ergeben sich aus den Verbindugnsvektoren  und und 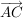 . .
Der Normalenvektor 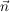 ist der Vektor, der zu ist der Vektor, der zu 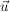 und und 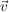 orthogonal ist. orthogonal ist.
Damit gilt:
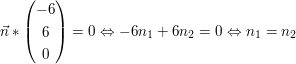
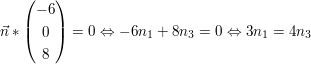
Da man eine Komponente frei wählen darf, setze 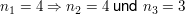
also erhält man
1. c) Gleichung der Innenwinkelhalbierenden w des Winkels BCA
zur Erinnerung: A(6;0;0), B(0;6;0), C(0;0;8)
Die Richtungen der beiden Schenkel dieses Winkels 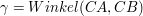 , also Winkel bei C, sind bekannt. , also Winkel bei C, sind bekannt.
Normiert man beide Vektoren auf Einheitsvektoren, ergeben sie aneinandergesetzt und ergänzt eine Raute (nur so als Vorstellung).
Die Diagonale dieser Raute ist zugleich die Winkelhalbierende von 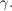
Es gilt also:
konkret:
Gleichung der Innenwinkelhalbierenden
Die Winkelhalbierende geht durch C (0;0;8) und hat die Richtung 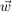 : :
Gleichung der Geraden durch A und B:
Schnittpunkt beider Geraden:
Der Schnittpnkt der Winkelhalbierenden mit der unteren Trapezseite ist S (3;3;0), die Mitte dieser Seite, wie man leicht nachrechnet. Außerdem gilt:
Die Winkelhalbierende ist parallel zur linken Trapezseite.
2. a) Die Punkte A, B, C und der Ursprung 0 bilden eine Pyramide. Berechen Sie das Volumen dieser Pyramide!
zur Erinnerung: A(6;0;0), B(0;6;0), C(0;0;8)
Volumen einer Pyramide:
mit G Grundfläche, hier das Dreieck ABC, und h Höhe, hier der Abstand der Ebene E(A,B,C) vom Ursprung.
Grundfläche G
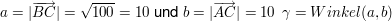
Winkel zwischen zwei Vektoren: 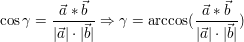
Damit ergibt sich schließlich:
Höhe der Pyramide
Abstand Punkt-Ebene: 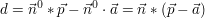 mit der Hesse-Form der Ebenengleichung. mit der Hesse-Form der Ebenengleichung.
Damit ergibt sich schlussendlich das Volumen:
2. b) Trapez
Zeigen Sie, dass das Viereck ABCD ein Trapez ist; zur Erinnerung: A(6;0;0), B(0;6;0), C(0;0;8), D (3;-3;8)
Jedes Trapez besitzt genau ein Paar paralleler Seiten.
Die Prüfung auf Parallelität der Vierecksseiten ergibt: 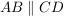
Die obere Seite ist halb so lang wie die untere, die angegebenen Vektoren sind entgegengesetzt gerichtet.
Damit zugleich gezeigt, dass die vier Punkte in einer Ebene liegen!
Das könnte man auch dadurch prüfen, indem man durch Punktprobe zeigt: D liegt in E(A,B,C).
Flächeninhalt des Trapez
3. Schnittgerade zweier Ebenen
Die Ebene E': x+y-z-6=0 schneidet die Ebene E (siehe Aufgabe 1b) in einer Geraden s. Zeigen Sie, dass s=AB gilt.
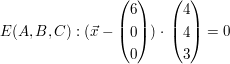
An den Normalenvektoren der beiden Ebenen liest man unmittelbar ab, dass sie nicht parallel sind.
Zu lösen ist das Gleichungssystem:
Dieses LGS ist erwartungsgemäß unterbestimmt, man kann eine Variable frei wählen: 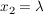
Damit ergibt sich dann als Schnittgerade:
Vergleich mit Gerade g(A,B):
alles ok
|