ParameteraufgabenGegeben ist die Funktion mit 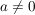 : :
An welchen Stellen des Definitionsbereichs gibt es 2 zueinander parallele Tangenten?
Welche Steigungen sind möglich?
Zeige, dass der Graph einer jeden Funktion 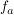 mit mit
die x-Achse berührt und bestimme alle weiteren Nullstellen.
Durch 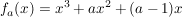 ist eine Kurvenschar gegeben. ist eine Kurvenschar gegeben.
Weise rechnerisch nach, dass alle Funktionen der Kurvenschar genau zwei Punkte gemeinsam haben und gib diese an.
Gegeben ist 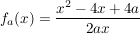 . .
M (4|0,5) ist Schnittpunkt der Funktionsgraphen.
Es ist zu überprüfen, für welche 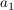 und und 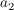 die Graphen orthogonal zueinander sind. die Graphen orthogonal zueinander sind.
Gegeben sind die Funktionen 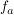 mit mit 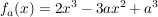 , ( , (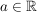 ) )
Zeige, dass für 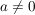 alle Funktionen der Schar die x-Achse berühren. alle Funktionen der Schar die x-Achse berühren.
Für 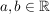 ist die Funktion ist die Funktion 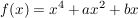 gegeben. gegeben.
a) Bestimme a und b so, dass der Graph von f an der Stelle 1 einen Sattelpunkt hat.
b) Für welche Parameter a und b hat der Graph von f keinen Wendepunkt?
Gegeben sei eine Kurvenschar 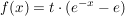 . .
Der Punkt ![$ P[u |t\cdot{}(e^{-u}-e)] $ $ P[u |t\cdot{}(e^{-u}-e)] $](/teximg/7/7/00388177.png) sei ein beliebiger Punkt auf jeder Kurve der Schar im 4. Quadranten. sei ein beliebiger Punkt auf jeder Kurve der Schar im 4. Quadranten.
Die Parallelen zu den Koordinatenachsen durch P bilden mit der y-Achse und der zugehörigen Asymptotenfunktion a(x)=-t*e ein Rechteck.
Bestimme die Maßzahl des maximalen Flächeninhaltes des Rechtecks.
Bestimme die Punkte 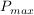 für den maximalen Flächeninhalt. für den maximalen Flächeninhalt.
Auf welcher Ortlinie liegen diese Punkte 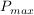 ? ?
|