VektorproduktDefinition Vektorprodukt
Schule
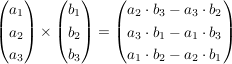
Hat man zwei Vektoren 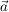 und und  , ,
ergibt der Vektor 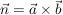 einen Vektor, der Senkrecht auf einen Vektor, der Senkrecht auf 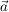 und und  steht. steht.
(Der Beweis läuft über das Skalarprodukt; es gilt:
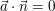 und und 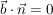 ) )
Dieses ist sehr hilfreich, wenn man eine Ebene in Parameterform in Normalenform umwandeln will, dann ist der Normalenvektor mit dem Vektorprodukt der beiden Richtungsvektoren schnell ermittelt.
Eine weitere Möglichkeit das Vektorprodukt (auch Kreuzprodukt) zu ermitteln besteht über eine 3x3-Determinante.

Nun ersetzt man
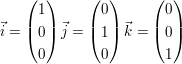 (Das sind die kanonischen Einheitsvekotren des (Das sind die kanonischen Einheitsvekotren des 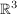 ) )
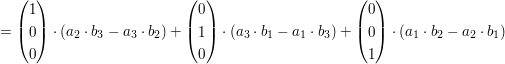
Nun fasst man alles zusammen und erhält folgenden Vektor:
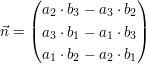
Universität
Links
![Link auf "http://de.wikipedia.org/wiki/Vektorprodukt" [link]](/images/popup.gif) http://de.wikipedia.org/wiki/Vektorprodukt http://de.wikipedia.org/wiki/Vektorprodukt
|