KegelDefinition Kegel
Schule
Rotiert ein rechtwinkliges Dreieck ABC um eine seiner Katheten als Drehachse, so entsteht ein gerader Kreiskegel.
Die Hypotenuse, die während der Drehung den Kegelmantel M bildet, heißt Mantellinie s. Die andere Kathete beschreibt die kreisförmige Grundfläche G. Alle Mantellinien treffen sich in der Spitze S des Kegels. Der Abstand der Spitze von der Grundfläche heißt Höhe h des Kegels.
Berechnung der Mantellinie
... durch Anwendung des Satz des Pythagoras:
Berechnung der Mantelfläche
Die Mantelfläche ergibt sich nach Aufschneiden längs einer Mantellinie und Ausbreiten in die Ebene als Kreissektor, dessen Radius R die Mantellinie s des Kegels ist und dessen Bogenlänge b mit dem Umfang  des Grundkreises übereinstimmt, d.h. es gilt: des Grundkreises übereinstimmt, d.h. es gilt:
Addiert man zur Mantelfläche noch die Grundfläche 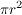 , so ergibt sich die Oberfläche O des Kegels: , so ergibt sich die Oberfläche O des Kegels:
Berechnung des Volumen
siehe auch: ![Link auf "http://de.wikipedia.org/wiki/Kegel_(Geometrie)" [link]](/images/popup.gif) Wikipedia: Kegel Wikipedia: Kegel
Universität
|