HurwitzkriteriumDie Stabilität eines Systems kann unter bestimmten Voraussetzungen mit dem Hurwitzpolynom ermittelt werden.
Hurwitzpolynom:
Unter dem Hurwitzpolynom versteht man das Nennerpolynom der Übertragungsfunktion.
Um die Stabilität zu gewährleisten, müssen in dem Polynom folgende Eigenschaften gegeben sein:
- alle Koeffizienten sind von Null verschieden:
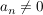
- alle Koeffizienten
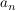 haben positive Vorzeichen haben positive Vorzeichen
- alle Hurwitz-Determinanten sind größer Null
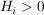
Hurwitzpolynom allg.: 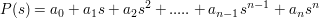
Beispiel:
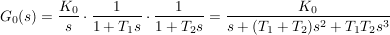
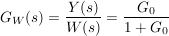

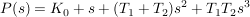
für die Koeffizienten folgt
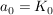
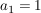
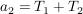
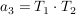
Annahme: 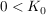
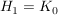
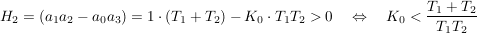
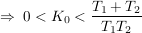
zurück
|