Hornerschema
Schule
Das Horner-Schema vereinfacht die Berechnung von Funktionswerten
Beispiel anhand einer Polynomfunktion 3.Grades
Die allgemeine Darstellung einer Polynomfunktion 3.Grades lautet
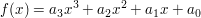
Ist von dieser Funktion eine Nullstelle  bekannt, so lässt sich der Linearfaktor bekannt, so lässt sich der Linearfaktor 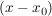 abspalten und die Funktion 3.Grades geht in eine Funktion 2.Grades ohne Restpolynom r(x) über abspalten und die Funktion 3.Grades geht in eine Funktion 2.Grades ohne Restpolynom r(x) über
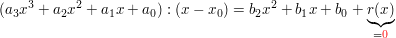
Die Bestimmung der Koeffizienten des reduzierten Polynoms erfolgt nach folgender Systematik
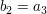
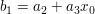
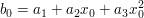
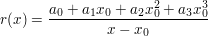
Das Verfahren ist nicht nur gültig für Polynome beliebiger Ordnung sondern auch für Stellen, welche keine Nullstellen sind.
Zahlenbeispiel
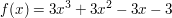
Man findet leicht eine Nullstelle bei 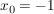
Dann ist
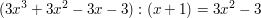
weil
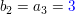
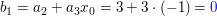
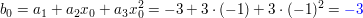
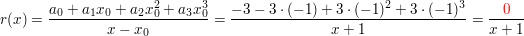
Nun das gleiche Beispiel noch einmal, wobei diesmal 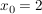 gewählt ist (keine Nullstelle der Funktion) gewählt ist (keine Nullstelle der Funktion)
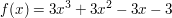
Dann ist
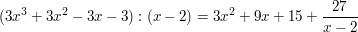
weil
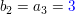
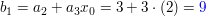
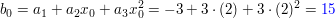
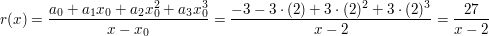
gute Erklärungen:
![Link auf "http://members.chello.at/gut.jutta.gerhard/kurs/horner.htm" [link]](/images/popup.gif) http://members.chello.at/gut.jutta.gerhard/kurs/horner.htm http://members.chello.at/gut.jutta.gerhard/kurs/horner.htm
![Link auf "http://www.zum.de/Faecher/M/NRW/pm/mathe/horner.htm" [link]](/images/popup.gif) http://www.zum.de/Faecher/M/NRW/pm/mathe/horner.htm http://www.zum.de/Faecher/M/NRW/pm/mathe/horner.htm
|