WachstumsfunktionDas Wachstums- oder Zerfallsgesetz lautet allgemein:
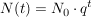
wobei  der Bestand zu Beginn der Betrachtung (t=0) ist und q(>1) der Wachstums- bzw. (0<q<1) der Zerfallsfaktor ist.
Für die Halbwertszeit T gilt nun:
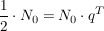 (nach T Jahren haben wir noch einen Bestand von  )
Beispiel
Die Zeitspanne, in der die Hälfte eines radioaktiven Stoffes zerfällt, heißt Halbwertszeit. Das Kohlenstoff-Isotop 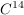 hat eine Halbwertszeit von 5730 Jahren.
Stelle das Zerfallsgesetz auf.
Wieviel Prozent einer vorhandenen Stoffmenge zerfällt jeweils in 100 Jahren?
Hier setze ich nun T=5730 ein und erhalte (nach Kürzen von ):
 (auf beiden Seiten  )
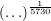Das ist nun ein Wert, den ihr mit dem Taschenrechner ausrechnen könnt.
Das Zerfallsgesetz lautet jetzt:
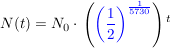 (das sieht kompliziert aus, ich habe aber keine Lust, den blauen Ausdruck mit dem TR auszurechnen ;-))
Der Bestand nach 100 Jahren berechnet sich jedenfalls durch Einsetzen des Zeitpunktes t=100 in das Zerfallsgesetz:
Hier muß ich wohl doch mal den TR bemühen und erhalte:
Diese bedeutet aber gerade:
Nach 100 Jahren beträgt der Bestand das 0,988-fache des Anfangsbestandes, in Prozenten: Nach 100 Jahren ist immer noch 98,8% des Anfangsbestandes vorhanden, nach 100 Jahren zerfällt also 1,2%.
Nun war aber nicht nur danach gefragt, wieviel Prozent im 100. Jahr zerfallen ist, sondern wie viel Prozent innerhalb beliebiger 100 Jahre --z.B. zwischen dem 2000. und 2100. Jahr-- zerfällt; bei einem exponentiellen Zerfall zerfällt aber über immer in derselben Zeitspanne derselbe prozentuale Anteil der Menge, d.h. für diese Aufgabe:
Während 100 Jahren zerfällt 1,2% des Isotops.
| 
