KonvergenzDefinition Grenzwert
Eine Zahl g heißt Grenzwert der Zahlenfolge 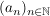 , ,
wenn nach Vorgabe irgendeiner positiven (kleinen) Zahl  fast alle Folgenglieder die Ungleichung fast alle Folgenglieder die Ungleichung 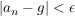 erfüllen. erfüllen.
"Fast alle" bedeutet dabei, dass es nur endlich viele Ausnahmen gibt.
Analog dazu spricht man auch vom Grenzwert einer Funktion
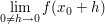 ,
dabei stellt man sich vor, dass man feststellen möchte, welchen (festen) Wert f an der Stelle  annimmt, obwohl man annimmt, obwohl man 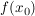 nicht ausrechnen kann, weil vielleicht nicht ausrechnen kann, weil vielleicht  nicht zum Definitionsbereich der Funktion gehört. nicht zum Definitionsbereich der Funktion gehört.
(siehe auch Differenzenquotient, stetig )
Anders gesagt:
In jeder noch so kleinen Umgebung von g liegen "fast alle" Folgenglieder.
Man schreibt dann: 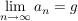 . .
Wenn eine Folge einen Grenzwert besitzt, dann nennt man sie konvergent.
In mathematischen Symbolen:
Sei 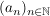 eine Zahlenfolge. Dann heißt eine Zahlenfolge. Dann heißt 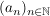 konvergent, falls: konvergent, falls:
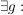 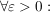 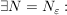  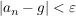 . .
Wenn sie keinen Grenzwert besitzt, nennt man sie divergent.
(Bemerkung: Die Folge 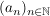 heißt also divergent (oder nicht konvergent), heißt also divergent (oder nicht konvergent),
falls:
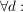 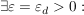 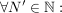 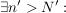 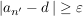 .) .)
Bemerkungen.
1.) Folgen, die als Grenzwert 0 haben, nennt man Nullfolgen.
2.) Eine (reell- oder komplexwertige) Folge  konvergiert genau dann, wenn es ein konvergiert genau dann, wenn es ein 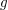 in in 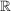 so gibt, dass so gibt, dass 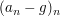 (oder (oder 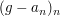 ) eine Nullfolge ist. ) eine Nullfolge ist.
Insbesondere gilt: Genau dann gilt 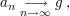 wenn wenn 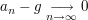 (bzw. (bzw.  ). ).
3.) Es sei (X,d) ein metrischer Raum. Dann heißt eine Folge 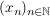 in X konvergent, falls: in X konvergent, falls:
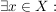 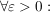 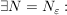  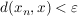 . .
Hierbei heißt 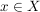 der Grenzwert der Folge der Grenzwert der Folge 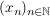 und ist eindeutig bestimmt, denn: und ist eindeutig bestimmt, denn:
Seien 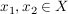 Grenzwerte der Folge Grenzwerte der Folge 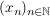 in X und es sei in X und es sei 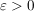 gegeben. Wir setzen gegeben. Wir setzen 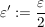 . .
Dann existiert ein 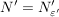 , so dass gilt: , so dass gilt:
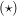 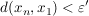 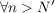 . .
Weiter existiert ein 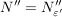 , so dass gilt: , so dass gilt:
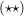 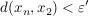  . .
Also gilt für alle 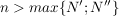 : :
 . .
Da 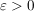 beliebig war, folgt: beliebig war, folgt:
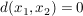 und damit und damit 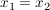 . . 
(Ergänzung zu dem Beweis:
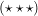 Wenn für Wenn für 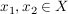 gilt, dass für alle gilt, dass für alle 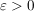 die Ungleichung die Ungleichung 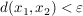 erfüllt ist, dann folgt daraus, dass erfüllt ist, dann folgt daraus, dass 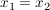 gilt. gilt.
Denn:
Es gelte 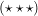 und angenommen, es wäre und angenommen, es wäre  . Dann folgt: . Dann folgt:
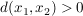 . Wir setzen . Wir setzen 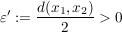 und erhalten: und erhalten:
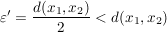 . Mit anderen Worten: . Mit anderen Worten:
Wir haben ein 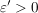 gefunden, so dass gefunden, so dass 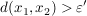 gilt im Widerspruch zu gilt im Widerspruch zu 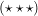 . .  ) )
siehe auch: Grenzwertsätze
|