Funktionsuntersuchung2Untersuche die Funktion f mit
Die Funktion  ist nur dann definiert, wenn die Nennerfunktion ist nur dann definiert, wenn die Nennerfunktion  ist. ist.
Wenn die Zählerfunktion 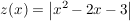 eine gemeinsame Nullstelle mit eine gemeinsame Nullstelle mit 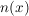 hat, handelt es sich evtl. um eine hebbare Stelle, d.h. es gibt eine stetige Fortsetzung der Funktion hat, handelt es sich evtl. um eine hebbare Stelle, d.h. es gibt eine stetige Fortsetzung der Funktion  . .
Man erhält die möglichen Definitionslücken, indem man 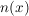 auf Nullstellen untersucht. auf Nullstellen untersucht.
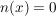  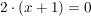    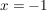
Es gilt 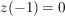 . D.h. die Definitionslücke könnte hebbar sein. Dazu müsste man der Funktion . D.h. die Definitionslücke könnte hebbar sein. Dazu müsste man der Funktion  an für an für 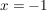 einen Wert zuweisen, so dass die Funktion in einen Wert zuweisen, so dass die Funktion in 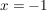 stetig ist. stetig ist.
Da 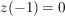 , erkennt man leicht die Faktorisierung , erkennt man leicht die Faktorisierung 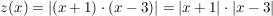 . .
Es wird also eine Fallunterscheidung durchgeführt für:
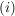 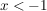  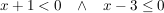  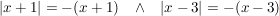
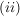 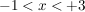  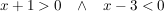  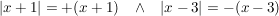
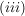 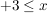  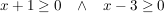  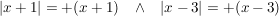
Damit erhält man auch folgende Darstellung der Funktion und kann entsprechend kürzen:
![$ f(x)= \frac{\left|(x+1)\cdot{}(x-3)\right|}{2\cdot{}(x+1)} = \begin{cases} \frac{[-(x+1)]\cdot{}[-(x-3)]}{2\cdot{}(x+1)} = \frac{(x+1)\cdot{}(x-3)}{2\cdot{}(x+1)} = \frac{x-3}{2} = \frac{1}{2}x-\frac{3}{2} , & \mbox{für } x<-1 \mbox{ } \\ \frac{[+(x+1)]\cdot{}[-(x-3)]}{2\cdot{}(x+1)} = \frac{-(x+1)\cdot{}(x-3)}{2\cdot{}(x+1)} = -\frac{x-3}{2} = -\frac{1}{2}x+\frac{3}{2} , & \mbox{für } -1<x<+3 \mbox{ } \\ \frac{[+(x+1)]\cdot{}[+(x-3)]}{2\cdot{}(x+1)} = \frac{(x+1)\cdot{}(x-3)}{2\cdot{}(x+1)} =\frac{x-3}{2} = \frac{1}{2}x-\frac{3}{2} , & \mbox{für } x\ge+3 \mbox{ } \end{cases} $ $ f(x)= \frac{\left|(x+1)\cdot{}(x-3)\right|}{2\cdot{}(x+1)} = \begin{cases} \frac{[-(x+1)]\cdot{}[-(x-3)]}{2\cdot{}(x+1)} = \frac{(x+1)\cdot{}(x-3)}{2\cdot{}(x+1)} = \frac{x-3}{2} = \frac{1}{2}x-\frac{3}{2} , & \mbox{für } x<-1 \mbox{ } \\ \frac{[+(x+1)]\cdot{}[-(x-3)]}{2\cdot{}(x+1)} = \frac{-(x+1)\cdot{}(x-3)}{2\cdot{}(x+1)} = -\frac{x-3}{2} = -\frac{1}{2}x+\frac{3}{2} , & \mbox{für } -1<x<+3 \mbox{ } \\ \frac{[+(x+1)]\cdot{}[+(x-3)]}{2\cdot{}(x+1)} = \frac{(x+1)\cdot{}(x-3)}{2\cdot{}(x+1)} =\frac{x-3}{2} = \frac{1}{2}x-\frac{3}{2} , & \mbox{für } x\ge+3 \mbox{ } \end{cases} $](/teximg/9/2/00488529.png)
Also ist der Definitionsbereich von  gegeben durch gegeben durch 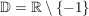 , da dieser Wert , da dieser Wert 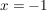 als Nullstelle des Nenners ausgeschlossen werden muss. als Nullstelle des Nenners ausgeschlossen werden muss.
Wie man bereits aus 1. weiß, handelt es sich bei dem Graphen von  um eine Funktion aus insgesamt drei Geradenabschnitten. um eine Funktion aus insgesamt drei Geradenabschnitten.
Kritisch für die Stetigkeit sind hier lediglich die beiden Intervallgrenzen bei 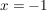 bzw. bzw. 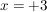 . .
An der Stelle 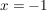 existiert kein Funktionswert. Es wird jedoch überprüft, ob es sich hierbei um eine hebbare Definitionslücke handelt: existiert kein Funktionswert. Es wird jedoch überprüft, ob es sich hierbei um eine hebbare Definitionslücke handelt:
![$ \lim_{x \to -1\uparrow} f(x)= \lim_{x \to -1\uparrow} \left[\frac{1}{2} \cdot (x-3)\right]=\frac{1}{2}\cdot{}(-1-3)=-2 $ $ \lim_{x \to -1\uparrow} f(x)= \lim_{x \to -1\uparrow} \left[\frac{1}{2} \cdot (x-3)\right]=\frac{1}{2}\cdot{}(-1-3)=-2 $](/teximg/9/7/00488579.png)
![$ \lim_{x \to -1\downarrow} f(x)= \lim_{x \to -1\downarrow} \left[-\frac{1}{2} \cdot (x-3)\right]=-\frac{1}{2}\cdot{}(-1-3)=+2 $ $ \lim_{x \to -1\downarrow} f(x)= \lim_{x \to -1\downarrow} \left[-\frac{1}{2} \cdot (x-3)\right]=-\frac{1}{2}\cdot{}(-1-3)=+2 $](/teximg/0/8/00488580.png)
Linksseitiger und rechtsseitiger Grenzwert an der Stelle 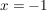 unterscheiden sich unterscheiden sich  die Definitionslücke bei die Definitionslücke bei 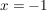 ist nicht hebbar; die Funktion ist nicht hebbar; die Funktion  ist bei ist bei 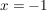 unstetig. unstetig.
Nun wird überprüft, ob an der Intervallgrenze 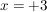 Stetigkeit vorliegt: Stetigkeit vorliegt:
![$ \lim_{x \to +3\uparrow} f(x)= \lim_{x \to +3\uparrow}\left[-\frac{1}{2}\cdot (x-3)\right]=-\frac{1}{2}\cdot{}(3-3)=0 $ $ \lim_{x \to +3\uparrow} f(x)= \lim_{x \to +3\uparrow}\left[-\frac{1}{2}\cdot (x-3)\right]=-\frac{1}{2}\cdot{}(3-3)=0 $](/teximg/7/7/00488577.png)
![$ \lim_{x \to +3\downarrow} f(x) = \lim_{x \to +3\downarrow} \left[\frac{1}{2} \cdot (x-3)\right]=\frac{1}{2}\cdot{}(3-3)=0=f(3) $ $ \lim_{x \to +3\downarrow} f(x) = \lim_{x \to +3\downarrow} \left[\frac{1}{2} \cdot (x-3)\right]=\frac{1}{2}\cdot{}(3-3)=0=f(3) $](/teximg/8/7/00488578.png)
Die Funktion  ist also an der Stelle ist also an der Stelle  stetig. stetig.
Wie man bereits aus 1. weiß, handelt es sich bei dem Graphen von  um eine Funktion aus insgesamt drei Geradenabschnitten. um eine Funktion aus insgesamt drei Geradenabschnitten.
Die Funktion  ist weder achsensymmetrisch zur ist weder achsensymmetrisch zur  -Achse, da -Achse, da  noch punktsymmetrisch zum Ursprung wegen noch punktsymmetrisch zum Ursprung wegen 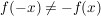 . .
4. Verhalten im Unendlichen
Die Funktion  verhält sich für sehr große sowie sehr kleine verhält sich für sehr große sowie sehr kleine  wie wie 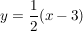 , daher gilt: , daher gilt:
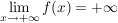 und und 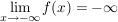
Aus 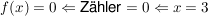 . .
Die 2. Nullstelle des Zählers bei 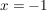 entfällt als Nullstelle, da diese nicht im Definitionsbereich enthalten ist. entfällt als Nullstelle, da diese nicht im Definitionsbereich enthalten ist.
Damit hat  als einzige Nullstelle: als einzige Nullstelle: 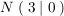
Die Funktion  wird über den Intervallen wird über den Intervallen 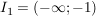 und und 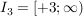 durch die ganzrationale Funktion durch die ganzrationale Funktion 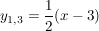 sowie im Intervall sowie im Intervall 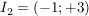 durch durch 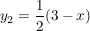 beschrieben und ist damit innerhalb dieser Intervalle stetig und beliebig oft differenzierbar. beschrieben und ist damit innerhalb dieser Intervalle stetig und beliebig oft differenzierbar.
Innerhalb der genannten Intervalle gilt also:
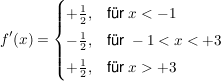
Da  an der Stelle an der Stelle 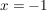 eine Unstetigkeitsstelle hat, ist sie dort auch nicht differenzierbar. eine Unstetigkeitsstelle hat, ist sie dort auch nicht differenzierbar.
Es bleibt zu zeigen, dass  auch für auch für 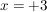 differenzierbar ist; sprich: der Differenzialquotient existiert. differenzierbar ist; sprich: der Differenzialquotient existiert.
Für den Grenzwert 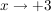 gilt: gilt:
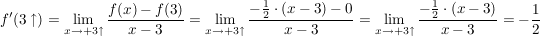
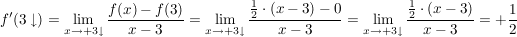
Die beiden Grenzwerte (linksseitig und rechtsseitig) unterscheiden sich. Von daher ist die Funktion an der Stelle 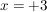 nicht differenzierbar. nicht differenzierbar.
Für die weiteren Ableitungen gilt also auch wieder nur innerhalb der o.g. Intervalle:
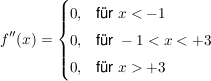
 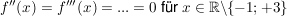
Notwendige Bedingung für Extrempunkte 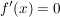 : Wegen : Wegen  hat hat  also keine Extremstellen. also keine Extremstellen.
Jedoch liegen an den Intervallgrenzen jeweils Randextrema vor, an deren Stelle keine horizontale Tangente vorliegt (siehe auch Skizze unten).
Notwendige Bedingung für Wendepunkte: 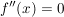
Wegen 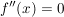 kommen alle kommen alle 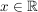 in Frage. in Frage.
Hinreichende Bedingung für Wendepunkte: 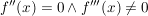
Wegen 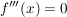 läßt sich aus der hinreichenden Bedingung keine Aussage treffen. Damit wird es nötig läßt sich aus der hinreichenden Bedingung keine Aussage treffen. Damit wird es nötig  aus einen Vorzeichenwechsel zu untersuchen. Da aus einen Vorzeichenwechsel zu untersuchen. Da  konstant konstant 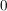 ist - und damit keine Vorzeichenwechsel hat - gibt es keinen Wendepunkt. ist - und damit keine Vorzeichenwechsel hat - gibt es keinen Wendepunkt.
9. Skizze

|