DefinitionslückeBeispiel für die Untersuchung einer Definitionslücke
einer reellen gebrochen-rationalen Funktion:
Offenbar ist die Funktion für die Werte 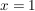 und und 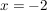 nicht definiert ist: nicht definiert ist: 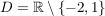 . .
Diese beiden Werte unterscheiden sich aber voneinander:
Während an der Stelle x=1 die Kurve lediglich ein "Loch" hat, eben eine Lücke, hat sie für x=-2 einen Pol.
Die erste Situation ist "behebbar", das heisst, man kann die Lücke schliessen, indem man einfach den Bruch durch (x-1) kürzt und anschließend x=1 "einsetzt"
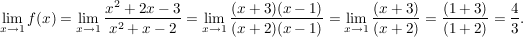
Dies geht an der anderen Stelle nicht, da der Graph einen "Sprung" macht von 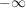 zu zu 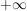 . .
Eine Definitionslücke liegt immer dann vor, wenn man für die gegebene Funktion keine "Ersatzfunktion" so finden kann, dass die Ersatzfunktion an allen Stellen des Definitionsbereichs mit der Funktion übereinstimmt und zusätzlich an der Lücke "stetig fortsetzbar" ist.
Wenn also bei den Grenzwerten von links 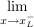 und von rechts und von rechts 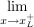 derselbe Grenzwert berechnet werden kann, die Funktion dort aber nicht definiert ist, dann definiert man die Ersatzfunktion als: derselbe Grenzwert berechnet werden kann, die Funktion dort aber nicht definiert ist, dann definiert man die Ersatzfunktion als:
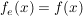 , für , für 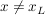 und und 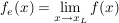 , für , für 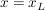
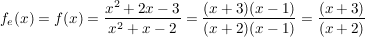 für für 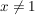 und und 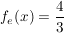 für für 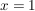 . .
Zur grafischen Darstellung:
Mir scheint, dies ist ab dem Moment ziemlich einfach, da man die Asymptoten kennt:
Sie werden hier wie ein Kreuz eingezeichnet. Die eine verläuft ja an der Stelle x=-2, also parallel zur y-Achse, die andere im Abstand 1 oberhalb der x-Achse und parallel zur x-Achse. Da die einzige Nullstelle bei x=-3 liegt, verläuft der eine "Ast" der Funktion "unten links" durch diese Nullstelle von der einen zur andern Asymptote, also im 2. und 3. Quadranten.
Für positive x-Werte verläuft der andere Ast entweder oberhalb oder unterhalb der x-Achse, und zwar auch von der einen zur andern Asymptote. Da es keine weitere Nullstelle gibt, kann der Graph die x-Achse nicht mehr schneiden. Um zu entscheiden, ob der Graph oberhalb oder unterhalb der x-Achse verläuft, setzen wir in der Gleichung für x eine günstige Zahl ein, zum Beispiel x=2: 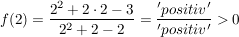 . .
Somit verläuft der Graph oberhalb der x-Achse.
Den genauen Wert braucht man nicht unbedingt; wichtig ist das Vorzeichen.
Die Asymptoten haben die Wirkung von "Leitplanken": Der Graph kommt ganz nahe an sie heran, ohne sie zu treffen.
Eine andere Überlegung ist die folgende:
In der Gleichung der "übrig gebliebenen" Funktion 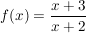 hat x im Nenner unten einen ungeraden höchsten Exponenten, nämlich 1. hat x im Nenner unten einen ungeraden höchsten Exponenten, nämlich 1.
Dies bedeutet auch, dass der Pol ein Pol "mit Zeichenwechsel" ist.
Das heisst: der Graph verläuft auf der einen Seite der senkrechten Asymptote ins negative Unendliche, auf der andern Seite ins positiv Unendliche.
Bei einen geraden höchsten Exponenten würden beide Äste auf der gleichen Seite liegen (beide im unendlich Positiven oder Negativen).
Zum schnellen Zeichnen von Funktionen empfehlen wir ![Link auf "http://www.funkyplot.de" [link]](/images/popup.gif) FunkyPlot. FunkyPlot.
|