Cramersche Regel Cramersche Regel
Sei 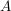 eine eine  -Matrix. Falls -Matrix. Falls 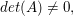 existiert eine explizite Determinantenformel für die Lösung existiert eine explizite Determinantenformel für die Lösung  eines gegebenen Gleichungssystems eines gegebenen Gleichungssystems 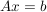 . .
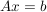 lässt sich als Linearkombination der Spalten der Matrix mit Koeffizienten lässt sich als Linearkombination der Spalten der Matrix mit Koeffizienten 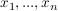 schreiben: schreiben:
Mittels Subtraktion des Vektors 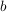 von dem i-ten Summanden folgt: von dem i-ten Summanden folgt:
Die Spalten der zugehörigen Matrix
sind also linear abhängig und die Determinante somit Null. Mit der Eigenschaft der Linearität der Determinante folgt:
Damit ist folgendes evident:
Satz
Ist 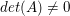 und und 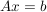 , dann gilt für , dann gilt für 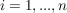 : :
Beispiel
Betrachte das lineare Gleichungssystem
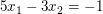

Die erweiterte Koeffizientenmatrix ist
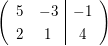 . .
Nach der Cramerschen Regel gilt:


Wie das Beispiel zeigt ist die Lösung linearer Gleichungssysteme mit Hilfe der Cramerschen Regel recht unpraktisch. Sie ist vielmehr im Hinblick auf den Zusammenhang der Veränderung von 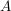 und und 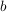 und der Lösung und der Lösung  interessant. Sie stellt somit ein wichtiges Instrument zur Untersuchung der durch interessant. Sie stellt somit ein wichtiges Instrument zur Untersuchung der durch 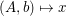 definierten Abbildung definierten Abbildung 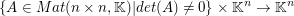 dar. dar.
Literatur
isbn9783540592235 K. Jänich: Lineare Algebra.
|