Benutzer:tobit09/Stochastik4Stochastisches Modellieren für Einsteiger
 3. Zähldichten p und Wahrscheinlichkeits-Verteilungen P 3. Zähldichten p und Wahrscheinlichkeits-Verteilungen P  Inhaltsverzeichnis Inhaltsverzeichnis
4. Zufallsvariablen 
a) Zufallsvariablen 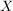
Unter einer Zufallsvariable zu einem stochastischen Vorgang in der realen Welt wollen wir etwas verstehen, was je nach Ausgang des stochastischen Vorganges einen Wert annimmt. Beispiele wären "Augensumme" oder "Augenzahl des ersten Würfels" beim zweifachen Würfelwurf.
Um von der zugehörigen mathematischen Zufallsvariable 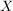 sprechen zu können, benötigen wir zunächst eine Ergebnismenge sprechen zu können, benötigen wir zunächst eine Ergebnismenge  , die den stochastischen Vorgang beschreibt. Dann verstehen wir unter der mathematischen Zufallsvariable , die den stochastischen Vorgang beschreibt. Dann verstehen wir unter der mathematischen Zufallsvariable 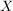 die Zuordnung (Abbildung), die jedem Ergebnis die Zuordnung (Abbildung), die jedem Ergebnis 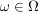 den Wert zuordnet, den die Zufallsvariable aus der realen Welt bei Eintreten von Ausgang den Wert zuordnet, den die Zufallsvariable aus der realen Welt bei Eintreten von Ausgang 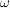 annimmt. annimmt.
Beispiel: Zufallsvariablen "Augensumme" und "Augenzahl des ersten Würfels" beim zweifachen Würfelwurf
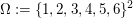
Bei Eintreten eines Ergebnisses 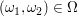 nimmt die Zufallsvariable "Augensumme" den Wert nimmt die Zufallsvariable "Augensumme" den Wert 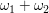 und die Zufallsvariable "Augenzahl des ersten Würfels" den Wert und die Zufallsvariable "Augenzahl des ersten Würfels" den Wert 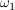 an. Die angenommenen Werte sind jeweils natürliche Zahlen. an. Die angenommenen Werte sind jeweils natürliche Zahlen.
Die zugehörigen mathematischen Zufallsvariablen lauten also
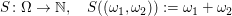
bzw.
 . .
Aufgabe 10: Beim Glücksrad mit den Feldern Niete, Trostpreis und Hauptpreis habe der Trostpreis einen Wert von 1 Euro und der Hauptpreis einen Wert von 10 Euro. Die Niete ist natürlich 0 Euro wert. Geben Sie die Zufallsvariable "Wert des Gewinns in Euro" als Abbildung an.
Lösungsvorschlag
b) Beschreibung von Ereignissen mit Zufallsvariablen
Beispiel: Ereignis "Augensumme=4" beim zweifachen Würfelwurf
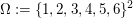
Sei 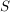 wie oben die Abbildung, die die Zufallsvariable "Augensumme" beschreibt. Dann tritt das Ereignis "Augensumme=4" bei Ausgang wie oben die Abbildung, die die Zufallsvariable "Augensumme" beschreibt. Dann tritt das Ereignis "Augensumme=4" bei Ausgang 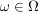 genau dann ein, wenn genau dann ein, wenn 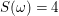 gilt. Damit lässt sich das Ereignis "Augensumme=4" schreiben als gilt. Damit lässt sich das Ereignis "Augensumme=4" schreiben als
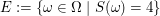 . .
(Es gilt  .) .)
Wir schreiben als abkürzende Notation 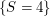 für dieses Ereignis. für dieses Ereignis.
Genauso können wir für beliebige Zufallsvariablen 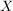 (die Zahlen als Werte annehmen) Ereignisse wie (die Zahlen als Werte annehmen) Ereignisse wie
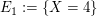
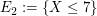
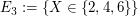
erklären. Sie stehen dafür, dass 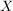 den Wert 4 bzw. einen Wert den Wert 4 bzw. einen Wert 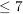 bzw. einen Wert bzw. einen Wert 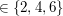 annimmt. Mathematisch handelt es sich dabei um die Mengen annimmt. Mathematisch handelt es sich dabei um die Mengen
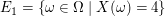
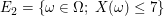
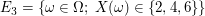 . .
Aufgabe 11: Beschreiben Sie die folgenden Ereignisse mithilfe von Zufallsvariablen. Geben Sie dazu jeweils sowohl die abkürzende Notation als auch deren Bedeutung an.
(i) "Zuerst eine 6 gewürfelt" beim zweifachen Würfelwurf
(ii) "keine Niete" beim Glücksrad aus Aufgabe 10 (mithilfe der Zufallsvariable "Wert des Gewinns in Euro" aus Aufgabe 10)
Lösungsvorschlag
|