Benutzer:tobit09/Beweis-Tutorial VorbereitungenBeweis-Tutorial
 Inhaltsverzeichnis Inhaltsverzeichnis  2. "es existiert"-Aussagen 2. "es existiert"-Aussagen
1. Vorbereitungen: Definitionen
Herzlich Willkommen zum Beweis-Tutorial!
Mal angenommen, wir wollen folgenden Zusammenhang beweisen:
Sei  eine gerade natürliche Zahl. Dann ist auch die natürliche Zahl eine gerade natürliche Zahl. Dann ist auch die natürliche Zahl 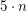 gerade. gerade.
Man nennt die zu Beginn getroffenen Annahmen (hier:  ist eine gerade natürliche Zahl) die Voraussetzungen und die zu beweisende Folgerung (hier: ist eine gerade natürliche Zahl) die Voraussetzungen und die zu beweisende Folgerung (hier: 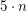 ist gerade) die Behauptung. ist gerade) die Behauptung.
Eigentlich eine Binsenweisheit, aber trotzdem von vielen nicht beachtet: Man kann kaum einen erfolgreichen Beweis führen, wenn man sich nicht klargemacht hat, was die Voraussetzungen und die Behauptung bedeuten.
Im obigen Beispiel müssen wir also zunächst wissen, wann eine natürliche Zahl gerade heißt. Hier die entsprechende Definition:
Definition Eine natürliche Zahl  heißt gerade, wenn eine natürliche Zahl heißt gerade, wenn eine natürliche Zahl  mit mit 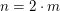 existiert. existiert.
Zurück zu obiger Beweis-Aufgabe: Die Voraussetzung " gerade" bedeutet also: gerade" bedeutet also:
Es existiert eine natürliche Zahl  mit mit 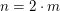 . .
Das dürfen wir für unseren Beweis also als gegeben annehmen und verwenden. Die Behauptung "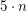 gerade" bedeutet: gerade" bedeutet:
Es existiert eine natürliche Zahl  mit mit  . .
Das müssen wir also zeigen. Da nicht zu erwarten ist, dass die Zahl  aus der Behauptung die gleiche ist wie die Zahl aus der Behauptung die gleiche ist wie die Zahl  aus der Behauptung, sollten wir besser in unserer Ausformulierung der Behauptung einen anderen Namen für diese Zahl wählen, z.B. aus der Behauptung, sollten wir besser in unserer Ausformulierung der Behauptung einen anderen Namen für diese Zahl wählen, z.B. 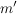 : :
Es existiert eine natürliche Zahl 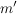 mit mit 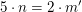 . .
Zusammengefasst:
Gegeben:
Eine natürliche Zahl  . .
Es existiert einen natürliche Zahl  mit mit 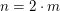 . .
Zu zeigen:
Es existiert eine natürliche Zahl 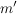 mit mit 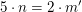 . .
Im Studium wirst du die Definitionen meist in deinen Vorlesungsmitschriften finden. Rekapituliere also alle benötigten Definitionen bzw. schlage sie nach. Schreibe dir am besten für jede einzelne Voraussetzung und für die Behauptung auf, was sie bedeutet, wie wir es für obiges Beispiel gemacht haben.
Für die Zwecke dieses Tutorials findest du alle benötigten Definitionen nachfolgend. In den zugehörigen kleinen Übungsaufgaben sollst du Routine im Anwenden von Definitionen bekommen. Denn wie gesagt: Um erfolgreich Beweise finden zu können, wirst du dir meist zunächst die Bedeutung der beteiligten Aussagen anhand der Definitionen klarmachen müssen. Den eigentlichen Beweisen widmen wir uns dann auf den nächsten Seiten.
Definition Seien  und und  natürliche Zahlen. Dann schreiben wir natürliche Zahlen. Dann schreiben wir 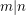 ( ( teilt teilt  ), falls eine natürliche Zahl ), falls eine natürliche Zahl 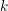 mit mit 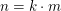 existiert. existiert.
Aufgabe 1 Seien  natürliche Zahlen. Was bedeutet die Aussage " natürliche Zahlen. Was bedeutet die Aussage "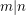 und und 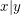 "? Lösungsvorschlag "? Lösungsvorschlag
Wenn im Folgenden von einer Funktion  die Rede ist, handelt es sich um eine "gewöhnliche" Funktion wie aus der Schule bekannt, die jeder reellen Zahl die Rede ist, handelt es sich um eine "gewöhnliche" Funktion wie aus der Schule bekannt, die jeder reellen Zahl  die reelle Zahl die reelle Zahl 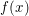 zuordnet. zuordnet.
Definition Eine Funktion  heißt gerade, falls heißt gerade, falls 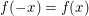 für alle reellen Zahlen für alle reellen Zahlen  gilt. gilt.
Eine Funktion  heißt ungerade, falls heißt ungerade, falls 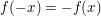 für alle reellen Zahlen für alle reellen Zahlen  gilt. gilt.
Aufgabe 2 Was bedeutet die folgende Aussage? "Die Funktion 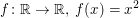 ist gerade." Lösungsvorschlag ist gerade." Lösungsvorschlag
Definition Eine Funktion  heißt monoton steigend, falls heißt monoton steigend, falls 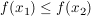 für alle reellen Zahlen für alle reellen Zahlen 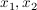 mit mit 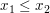 gilt. gilt.
Eine Funktion  heißt monoton fallend, falls heißt monoton fallend, falls 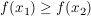 für alle reellen Zahlen für alle reellen Zahlen 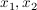 mit mit 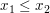 gilt. gilt.
Aufgabe 3 Sei 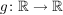 eine Funktion. Was bedeutet die Aussage " eine Funktion. Was bedeutet die Aussage "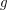 ist monoton fallend"? Lösungsvorschlag ist monoton fallend"? Lösungsvorschlag
Definition Eine Funktion  heißt surjektiv, falls für alle reellen Zahlen heißt surjektiv, falls für alle reellen Zahlen 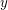 eine reelle Zahl eine reelle Zahl  mit mit 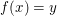 existiert. existiert.
Aufgabe 4 Was bedeutet die folgende Aussage? "Die Funktion 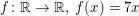 ist surjektiv." Lösungsvorschlag ist surjektiv." Lösungsvorschlag
|