Benutzer:tobit09/Beweis-Anleitung Beispiel-Teilmenge1Wie führe ich einen Beweis?
 5. Beispiele 5. Beispiele  b) Teilmengenbeziehung 2 b) Teilmengenbeziehung 2
5. Beispiele
a) Teilmengenbeziehung 1
Aufgabe:
Seien 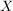 , , , ,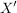 und und 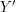 Mengen. Es gelte Mengen. Es gelte 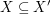 und und 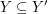 . Zeigen Sie, dass dann auch . Zeigen Sie, dass dann auch  gilt. gilt.
Vorbereitung des Beweises:
Voraussetzungen:
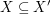 bedeutet: bedeutet:
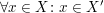 . .
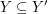 bedeutet: bedeutet:
 . .
Behauptung:
 . .
Dabei ist
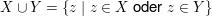
und
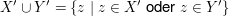 . .
Rahmen des Beweises:
Zu zeigen ist also eine Teilmengenbeziehung. Punkt i) unter 3. Wie zeige ich...? verrät uns, was zu tun ist: Wir betrachten ein beliebig vorgegebenes Element 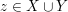 und zeigen unter der zusätzlichen Voraussetzung und zeigen unter der zusätzlichen Voraussetzung 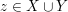 die Aussage die Aussage 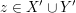 . .
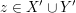 bedeutet, dass bedeutet, dass 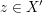 oder oder 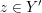 . Zu zeigen ist also diese "oder"-Aussage. Punkt b) unter 3. Wie zeige ich...? verrät uns, was zu tun ist: Wir müssen eine Fallunterscheidung nach gewissen Fällen . Zu zeigen ist also diese "oder"-Aussage. Punkt b) unter 3. Wie zeige ich...? verrät uns, was zu tun ist: Wir müssen eine Fallunterscheidung nach gewissen Fällen 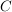 und und 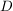 durchführen, für die durchführen, für die 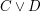 als wahr bekannt ist. Dann zeigen wir, dass aus als wahr bekannt ist. Dann zeigen wir, dass aus 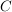 die Aussage die Aussage 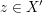 und aus und aus 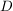 die Aussage die Aussage 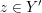 folgt. folgt.
Somit ergibt sich folgender Beweisrahmen:
Zu zeigen ist, dass  gilt. gilt.
Sei also 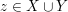 . .
Zu zeigen ist, dass 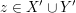 gilt, d.h. dass gilt, d.h. dass 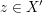 oder oder 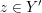 gilt. gilt.
...
Hauptteil
(1. Fall: 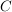 . Zeigen, dass in diesem Fall . Zeigen, dass in diesem Fall 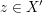 .) .)
(2. Fall: 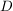 . Zeigen, dass in diesem Fall . Zeigen, dass in diesem Fall 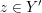 .) .)
...
Somit gilt in jedem Fall 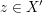 oder oder 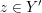 , also , also 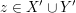 . .
Da 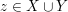 beliebig war, folgt beliebig war, folgt  . .
Hauptteil des Beweises:
Die Voraussetzungen 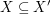 und und 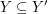 sind "für alle"-Aussagen. Punkt f) unter 4. Wie benutze ich...? rät uns, Elemente sind "für alle"-Aussagen. Punkt f) unter 4. Wie benutze ich...? rät uns, Elemente 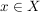 bzw. bzw. 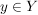 zu finden, für die wir dann auf zu finden, für die wir dann auf 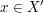 bzw. bzw. 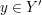 schließen können. Noch haben wir keine solchen Elemente schließen können. Noch haben wir keine solchen Elemente  und und  . .
Für den Hauptteil haben wir aber als zusätzliche Voraussetzung 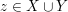 . Das bedeutet . Das bedeutet 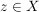 oder oder 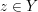 . Punkt b) in 4. Wie benutze ich...? legt uns für solche "oder"-Aussagen eine Fallunterscheidung nach . Punkt b) in 4. Wie benutze ich...? legt uns für solche "oder"-Aussagen eine Fallunterscheidung nach 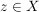 bzw. bzw. 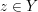 nahe. Und genau eine Fallunterscheidung haben wir bei unseren Gedanken zum Beweisrahmen ja gesucht! nahe. Und genau eine Fallunterscheidung haben wir bei unseren Gedanken zum Beweisrahmen ja gesucht!
Nehmen wir als 1. Fall also mal 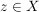 . Jetzt haben wir also endlich ein Element von . Jetzt haben wir also endlich ein Element von 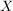 gefunden, auf das wir gefunden, auf das wir 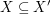 anwenden können: Wir können anwenden können: Wir können 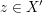 folgern. Und genau da wollten wir hin! folgern. Und genau da wollten wir hin!
Unser 2. Fall lautet 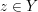 . Jetzt haben wir also ein Element von . Jetzt haben wir also ein Element von  gefunden, auf das wir gefunden, auf das wir 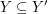 anwenden können: Wir können anwenden können: Wir können 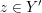 folgern. Und genau da wollten wir hin! folgern. Und genau da wollten wir hin!
Fertiger Beweis:
Zu zeigen ist, dass  gilt. gilt.
Sei also 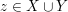 . .
Zu zeigen ist, dass 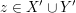 gilt, d.h. dass gilt, d.h. dass 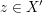 oder oder 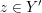 gilt. gilt.
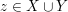 bedeutet, dass bedeutet, dass 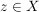 oder oder 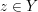 gilt. gilt.
1. Fall: 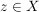 . Wegen . Wegen 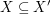 folgt dann folgt dann 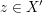 C'' C''
2. Fall: 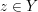 . Wegen . Wegen 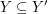 folgt dann folgt dann 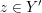 C'' C''
Somit gilt in jedem Fall 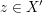 oder oder 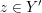 , also , also 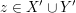 . .
Da 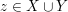 beliebig war, folgt beliebig war, folgt  . .
|