RegressionsgeradeEinleitung:
In vielen Zusammenhängen ist es sinnvoll, experimentelle oder statistische Daten durch einfache mathematische Modelle zu approximieren. Besonders wichtig - weil besonders einfach - sind dabei lineare Approximationen. Viele naturwissenschaftliche Gesetze beruhen auf Entdeckungen linearer oder doch wenigstens ungefähr linearer Zusammenhänge zwischen Messgrößen.
Deshalb ist die Aufgabe, zu einer Reihe von Datenpunkten eine möglichst gut passende Gerade zu finden, eine Standardaufgabe der Statistik.
Herleitung der Gleichung der Regressions- oder Ausgleichsgeraden:
Gegeben seien die Punkte
welche in der x-y-Ebene ungefähr geradlinig angeordnet sind.
Gesucht ist jene Gerade g , welche den linearen Zusammenhang bestmöglich approximiert. Das Kriterium dazu ergibt sich aus der Methode der kleinsten Fehlerquadrat-Summe von Carl Friedrich Gauß.
Die gesuchte Gerade g hat eine Gleichung der Form y=m*x+b .
Der Punkt  hat in y-Richtung den Abstand hat in y-Richtung den Abstand 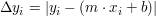 von der Geraden g. Nun soll die Summe der Quadrate dieser "Residuen" minimiert werden: von der Geraden g. Nun soll die Summe der Quadrate dieser "Residuen" minimiert werden:
Ausmultipliziert ergibt dies:
Diese Funktion 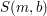 hat ( ausser im Fall hat ( ausser im Fall 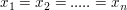 ) genau ein Extremum, und zwar ein Minimum, an der Stelle, wo die beiden partiellen Ableitungen verschwinden: ) genau ein Extremum, und zwar ein Minimum, an der Stelle, wo die beiden partiellen Ableitungen verschwinden:
Das entstandene Gleichungssystem kann man auch in dieser Form schreiben:
Auflösung nach der Cramerschen Regel:
Für die Praxis gibt es auch andere Berechnungsmethoden, bei welchen man z.B. von einer provisorisch gewählten Geraden ausgeht. Die Berechnung der Regressionsgeraden ist standardmässig in vielen graphischen Taschenrechnern eingebaut, und im Internet findet man viele Applets, die dies durchführen, zum Beispiel bei mathe-online.at.
Ein Rechenbeispiel:
Ausgleichsgerade durch n=5 Punkte
  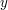   
1 3 8 9 24 64
2 6 7 36 42 49
3 9 3 81 27 9
4 13 4 169 52 16
5 15 2 225 30 4
SX= 46 SY= 24 SXX= 520 SXY= 175 SYY= 142
Gleichung der Ausgleichsgeraden: y = m x + b
Also g: y = - 0.473 x + 9.15
Alternative Berechnungsmethode:
Aus den oben hergeleiteten Formeln kann man einen anderen Formelsatz herleiten, bei welchem man zuerst die Mittelwerte 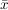 und und  bestimmt: bestimmt:
  
Vorteile dieser Methode:
Der gesamte Rechenaufwand ist zwar nur geringfügig kleiner als nach der anderen Methode, ein Vorteil besteht aber darin, dass die zu berechnenden Produkte im Allgemeinen deutlich kleiner sind.
Einschränkung:
Die oben dargestellte Methode der kleinsten Quadratsumme der in y-Richtung gemessenen Residuen  ist besonders dann geeignet, falls sich die Datenpunkte ist besonders dann geeignet, falls sich die Datenpunkte  ungefähr entlang einer Geraden mit einer kleinen Steigung |m| verteilen. Ist dies aufgrund der Sichtung des Datenmaterials nicht der Fall, ist es angezeigt, nach besseren Methoden Ausschau zu halten, um die Gerade zu bestimmen, welche die "Punktwolke" am besten approximiert bzw. linearisiert. Siehe dazu beispielsweise die folgende Forumsdiskussion: 469873 ungefähr entlang einer Geraden mit einer kleinen Steigung |m| verteilen. Ist dies aufgrund der Sichtung des Datenmaterials nicht der Fall, ist es angezeigt, nach besseren Methoden Ausschau zu halten, um die Gerade zu bestimmen, welche die "Punktwolke" am besten approximiert bzw. linearisiert. Siehe dazu beispielsweise die folgende Forumsdiskussion: 469873
Bemerkung: die dort beschriebene Methode der sukzessiven Approximation ist noch nicht das "Gelbe vom Ei". Eine exakte Methode benützt die Methode der Eigenvektoren.
|