ABCFormelSatz ABCFormel (auch Mitternachtsformel)
Die Lösung(en) einer quadratischen Gleichung der Form:
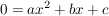 mit mit 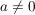 (Falls a = 0 , handelt es sich um keine quadratische, sondern eine lineare Gleichung) (Falls a = 0 , handelt es sich um keine quadratische, sondern eine lineare Gleichung)
lauten:
Falls 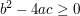 : :
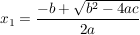
und
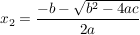 . .
In Kurzschreibweise:
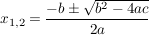 ; ;
falls 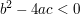 , hat die quadratische Gleichung keine Lösung. , hat die quadratische Gleichung keine Lösung.
Beweis.
Da nach Voraussetzung 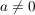 , gilt: , gilt:
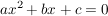

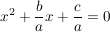
Wir setzen wegen der bereits bewiesenen p/q-Formel
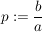 und und 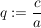 . .
Denn damit gilt:
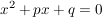

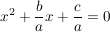 . .
Nach der (bereits bewiesenen) p/q-Formel erhalten wir also für 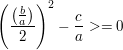 die Lösungen: die Lösungen:
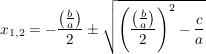

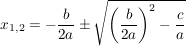

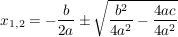

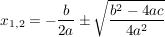

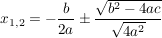

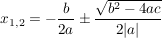 ; ;
falls 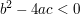 hat die quadratische Gleichung keine Lösung. hat die quadratische Gleichung keine Lösung.
1. Fall:
Ist nun 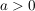 , so erhalten wir: , so erhalten wir:
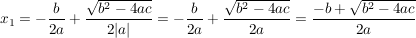 , ,
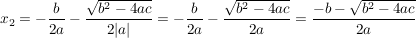 . .
Damit ist (sofern die Ausdrücke (wohl-)definiert sind) 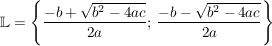 die Lösungsmenge der Gleichung die Lösungsmenge der Gleichung 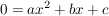 für alle für alle 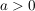 . .
2. Fall:
Ist nun 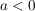 , so erhalten wir: , so erhalten wir:
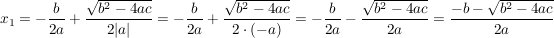 , ,
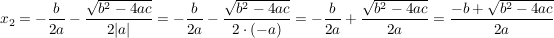 . .
Damit ist (sofern die Ausdrücke (wohl-)definiert sind) 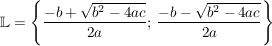 auch die Lösungsmenge der Gleichung auch die Lösungsmenge der Gleichung 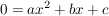 für alle für alle 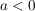 . .
Fazit:
Für alle 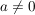 (und sofern die Ausdrücke (wohl-)definiert sind) ist also (und sofern die Ausdrücke (wohl-)definiert sind) ist also 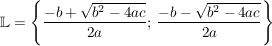
(in Kurzschreibweise: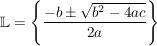 ) die Lösungsmenge der Gleichung ) die Lösungsmenge der Gleichung 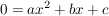 und die Behauptung ist gezeigt! und die Behauptung ist gezeigt! 
Bemerkungen.
Man versteht hier darunter, dass die Ausdrücke (wohl-)definiert sind, folgendes:
1.) 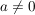 , weil man sonst durch Null teilen würde. , weil man sonst durch Null teilen würde.
2.) 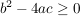 , denn der Ausdruck unter dem Wurzelzeichen darf nicht , denn der Ausdruck unter dem Wurzelzeichen darf nicht 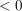 sein! sein!
Die Formel ist so wichtig, dass man sie selbst dann noch auswendig hersagen können sollte, wenn man mitternachts aus dem Tiefschlaf geweckt würde!
|