Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
Dietlind Bäro
Daniel Metzsch | www.matheraum.de
Mathe für's ABI 2008
Aufgabenblatt 2
Abgabe: Fr 16.11.2007 14:00 | 02.11.2007 | | Aufgabe 1 | Zugelassene Hilfsmittel: Tafelwerk
Im Koordinatensystem sind einige Graphen 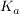 der Funktionenschar der Funktionenschar 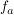 mit mit
 ; ; 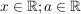
dargestellt.
1.1 Zeigen Sie, dass jeder Graph 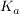 genau einen Wendepunkt genau einen Wendepunkt
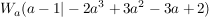
besitzt.
1.2 Bestimmen Sie eine Gleichung der Wendetangente
(Tangente im Wendepunkt) an 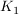 . .
Ein Graph der Schar 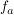 hat eine Wendetangente, deren Anstieg größer ist als der Ansteig aller anderen Wendepunkte an hat eine Wendetangente, deren Anstieg größer ist als der Ansteig aller anderen Wendepunkte an 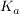 . .
Ermitteln Sie den zugehörigen Parameter a und geben Sie diesen größtmöglichen Anstieg an.
1.3 Ein Graph  und die x-Achse begrenzen zwei Flächen vollständig. und die x-Achse begrenzen zwei Flächen vollständig.
Ermitteln Sie das Verhältnis der beiden Flächeninhalte.
Für eine Kurve 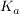 sind die beiden beschriebenen Flächen gleich groß. Bestimmen Sie a. sind die beiden beschriebenen Flächen gleich groß. Bestimmen Sie a.
|
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|