Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
| www.matheraum.de
Wahrscheinlichkeitstheorie (Bauer)
Aufgabenblatt 1
Abgabe: Mo 09.04.2007 14:00 | 02.04.2007 | | Dieser Übungszettel enthält die Aufgaben aus Kapitel I, § 2. Laplace-Experimente und bedingte Wahrscheinlichkeit | | Aufgabe 1 | Ein Würfel wird n-mal geworfen.
Mit welcher Wahrscheinlichkeit fällt genau beim n-ten Wurf zum k-ten Mal eine Vier (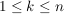 )? )? | | Aufgabe 2 | Drei Urnen 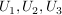 enthalten gut durchmischt schwarze, weiße und rote, sonst aber gleichartige Kugeln. Es enthalte enthalten gut durchmischt schwarze, weiße und rote, sonst aber gleichartige Kugeln. Es enthalte
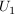 : 2 schwarze, 3 weiße, 5 rote Kugeln; : 2 schwarze, 3 weiße, 5 rote Kugeln;
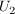 : 4 schwarze, 2 weiße, 4 rote Kugeln; : 4 schwarze, 2 weiße, 4 rote Kugeln;
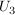 : 2 schwarze, 5 weiße, 3 rote Kugeln. : 2 schwarze, 5 weiße, 3 rote Kugeln.
(a) Aus der Urne 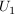 wird ohne Zurücklegen gezogen. wird ohne Zurücklegen gezogen.
Wie groß ist die Wahrscheinlichkeit dafür, dass die erste und zweite Kugel schwarz und die dritte Kugel weiß ist?
(b) Man bestimme die Wahrscheinlichkeit 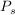 (bzw. (bzw. 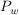 bzw. bzw. 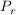 ) mit welcher nach vorausgehender zufälliger Wahl einer der Urnen eine schwarze (bzw. weiße bzw. rote) Kugel gezogen wird. ) mit welcher nach vorausgehender zufälliger Wahl einer der Urnen eine schwarze (bzw. weiße bzw. rote) Kugel gezogen wird.
Warum ist 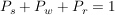 ? ?
(c) Mit welcher Wahrscheinlichkeit zieht man nach vorausgehender zufälliger Wahl einer der Urnen der Reihe nach 4 schwarze Kugeln ohne Zurücklegen?
Wie groß ist die Wahrscheinlichkeit dafür, dass diese 4 schwarzen Kugeln der Urne 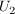 entstammen? entstammen? | | Aufgabe 3 | | Wie groß ist die Wahrscheinlichkeit, dass 10 zufällig ausgewählte Personen ihre Geburtstage in verschiedenen Monaten haben? | | Aufgabe 4 | Eine Urne enthält gut durchmischt gleichartige Kugeln in  verschiedenen Farben, nämlich verschiedenen Farben, nämlich 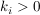 Kugeln der Farbe Kugeln der Farbe 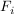 , , 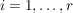 . .
Der Urne entnehme man in einem Zug  Kugeln, wobei Kugeln, wobei 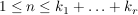 ist. ist.
Mit welcher Wahrscheinlichkeit zieht man genau 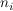 Kugeln der Farbe Kugeln der Farbe 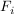 , , 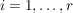 ? ?
Dabei sei 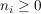 für alle für alle 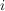 und und 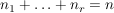 . . | | Aufgabe 5 | Eine Urne enthält gut durchmischt 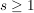 schwarze und schwarze und 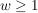 weiße Kugeln. Es wird ohne Zurücklegen gezogen. weiße Kugeln. Es wird ohne Zurücklegen gezogen.
Welches ist die Wahrscheinlichkeit, um in  Zügen mindestens Zügen mindestens  schwarze Kugeln zu erhalten ( schwarze Kugeln zu erhalten (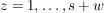 )? )? | | Aufgabe 6 | (Pólyasches Urnen-Modell)
Eine Urne enthält gut durchmischt 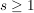 schwarze und schwarze und 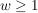 weiße Kugeln. Eine Kugel wird gezogen und wieder zurückgelegt; ferner werden weiße Kugeln. Eine Kugel wird gezogen und wieder zurückgelegt; ferner werden 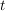 weitere Kugeln der Farbe der gezogenen Kugel in die Urne gelegt. Nach neuer Durchmischung wird wieder eine Kugel gezogen und obiges Verfahren mit gleicher Zahl weitere Kugeln der Farbe der gezogenen Kugel in die Urne gelegt. Nach neuer Durchmischung wird wieder eine Kugel gezogen und obiges Verfahren mit gleicher Zahl 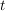 wiederholt. wiederholt.
Man zeige: Die Wahrscheinlichkeit in 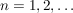 Zügen Zügen 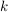 schwarze und schwarze und 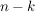 weiße Kugeln zu ziehen ist weiße Kugeln zu ziehen ist
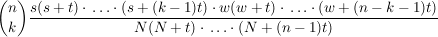
wenn dabei 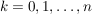 ist und ist und 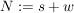 gesetzt wird. gesetzt wird.
Ist die unter 1 (b) beschriebene Situation hiervon ein Spezialfall?
Nachtrag: In 1(b) wurde folgendes Modell vorgestellt:
In einer Urne befinden sich gut durchmischt n gleichartige Kugeln in den Farben Schwarz und Weiß, etwa s schwarze und w weiße (s+w=n). Man zieht willkürlich 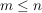 Kugeln und fragt nach der Wahrscheinlichkeit, dass darunter genau Kugeln und fragt nach der Wahrscheinlichkeit, dass darunter genau  schwarze Kugeln sind. Jede gezogene Kugel wird sofort wieder in die Urne zurückgelegt; nach erneutem Durchmischen des Urneninhaltes wird die nächste Kugel gezogen. [...] Die gesuchte Wahrscheinlichkeit beträgt schwarze Kugeln sind. Jede gezogene Kugel wird sofort wieder in die Urne zurückgelegt; nach erneutem Durchmischen des Urneninhaltes wird die nächste Kugel gezogen. [...] Die gesuchte Wahrscheinlichkeit beträgt 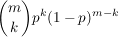 mit mit 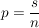 |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|