Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
Dipl. math. Felix Fontein
Dipl. math. Dieter Osterholz | www.matheraum.de
Algebra-Training 2006
Aufgabenblatt 4
Abgabe: Fr 06.10.2006 12:00 | 22.09.2006 | | Wie angekuendigt springen wir erstmal fuer den Abschnitt 5.1 nach Kapitel 5. | | Aufgabe 14 |
Sei G eine Gruppe, 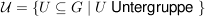 die Menge aller Untergruppen von G und die Menge aller Untergruppen von G und 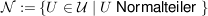 die Menge aller Normalteiler in G. die Menge aller Normalteiler in G.
(i) Zeige, dass 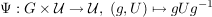 eine Operation von G auf eine Operation von G auf 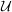 liefert. liefert.
(ii) Zeige, dass die Bahn eines Elementes 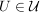 genau dann aus einem Element besteht, wenn U ein Normalteiler in G ist. genau dann aus einem Element besteht, wenn U ein Normalteiler in G ist.
(iii) Sei 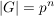 fuer eine Primzahl p und fuer eine Primzahl p und 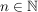 . Dann ist . Dann ist 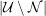 durch p teilbar. durch p teilbar.
| | Aufgabe 15 |
Sei G eine endliche Gruppe,  eine Untergruppe und eine Untergruppe und 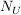 der Normalisator von U in G. Setze der Normalisator von U in G. Setze 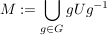 . .
(i) Beweise  . .
(ii) Sei 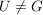 . Zeige, dass dann auch . Zeige, dass dann auch  ist. ist.
| | Aufgabe 16 |
Sei G eine Gruppe,  eine Untergruppe und eine Untergruppe und 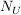 bzw. bzw. 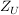 der Normalisator bzw. Zentralisator von U in G. Zeige, dass der Normalisator bzw. Zentralisator von U in G. Zeige, dass 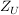 ein Normalteiler in ein Normalteiler in 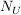 ist und dass ist und dass 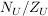 isomorph zu einer Untergruppe von der Automorphismengruppe isomorph zu einer Untergruppe von der Automorphismengruppe 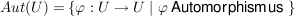 ist. ist.
| | Aufgabe 17 |
Sei G eine Gruppe mit 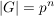 , wobei p eine Primzahl sei und , wobei p eine Primzahl sei und 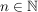 . Zeige, dass das Zentrum Z von G mindestens p Elemente umfasst. . Zeige, dass das Zentrum Z von G mindestens p Elemente umfasst.
Hinweis: Klassengleichung.
|
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|